题目内容
18.已知关于x,y的方程组$\left\{\begin{array}{l}{x+2y=5k-2}\\{x-y=-k+4}\end{array}\right.$的解满足x>0,y<0.(1)求k的取值范围;
(2)化简:|k+2|-|k-1|;
(3)设t=|k+2|-|k-1|,则t的取值范围是-3<t<3.
分析 (1)将k看作常数解方程组,根据x>0、y<0得关于k的不等式组,解不等式组可得k的取值范围;
(2)根据(1)中k的范围结合绝对值性质去绝对值符号化简即可;
(3)由(2)知t=|k+2|-|k-1|=2k+1,根据k的范围即可得2k+1的范围.
解答 解:(1)解方程组$\left\{\begin{array}{l}{x+2y=5k-2}\\{x-y=-k+4}\end{array}\right.$得:$\left\{\begin{array}{l}{x=k+2}\\{y=2k-2}\end{array}\right.$,
∵x>0,y<0,
∴$\left\{\begin{array}{l}{k+2>0}\\{2k-2<0}\end{array}\right.$,
解得:-2<k<1;
(2)∵-2<k<1,
∴k+2>0,k-1<0,
∴|k+2|-|k-1|=k+2+(k-1)
=2k+1;
(3)由题意知,t=|k+2|-|k-1|=2k+1,
∵-2<k<1,
∴-3<2k+1<3,
即-3<t<3.
故答案为:(3)-3<t<3.
点评 本题主要考查二元一次方程组的解及绝对值的性质,解方程组得到关于k的不等式组是解题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
9.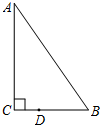 如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
 如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )| A. | 70° | B. | 70°或120° | C. | 120° | D. | 80° |
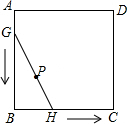 如图,正方形ABCD的边长为4,线段GH=AB,将GH的两端放在正方形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点H从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段GH的中点P所经过的路线围成的图形的面积为16-4π.
如图,正方形ABCD的边长为4,线段GH=AB,将GH的两端放在正方形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点H从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段GH的中点P所经过的路线围成的图形的面积为16-4π. 已知:如图,PC切⊙O于点C,PA交⊙O于点A,B.
已知:如图,PC切⊙O于点C,PA交⊙O于点A,B.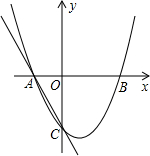 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线.
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线. 已知关于x的方程mx2-(3m-1)x+2m-2=0.
已知关于x的方程mx2-(3m-1)x+2m-2=0. 如图,已知正方形ABCD的边长为1,点E,F分别在边BC,CD上,且∠EAF=45°,则△CEF的周长为2.
如图,已知正方形ABCD的边长为1,点E,F分别在边BC,CD上,且∠EAF=45°,则△CEF的周长为2.