题目内容
15.若(x+3)(x+n)=x2+mx-21,则m的值为( )| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
分析 把(x+3)(x+n)展开得出x2+(n+3)x+3n,得出x2+mx-21=x2+(n+3)x+3n,推出m=n+3,-21=3n,求出即可.
解答 解:(x+3)(x+n)=x2+nx+3x+3n=x2+(n+3)x+3n,
∵x2+mx-21=(x+3)(x+n),
∴x2+mx-21=x2+(n+3)x+3n,
∴m=n+3,-21=3n,
解得:n=-7,m=-4,
故选D.
点评 本题多项式乘以多项式法则,解二元一次方程组等知识点,解决本题关键是能得出m=n+3,-21=3n.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
7.点(-1,-1)关于原点对称的点的坐标是( )
| A. | (-1,1) | B. | (1,1) | C. | (1,-1) | D. | (0,0) |
4.江津中学七年级准备开展“阳光体育 ”活动,为了丰富同学们的体锻内容,体育委员小灵到体育用品商店购买羽毛球拍和乒乓球拍,若购买1副羽毛球拍和1副乒乓球拍共需50元,小强一共用320元购买了6副同样的羽毛球拍和10副同样的乒乓球拍.若设每副羽毛球拍为x元,每副乒乓球拍为y元,列二元一次方程组得( )
| A. | $\left\{\begin{array}{l}{x+y=50}\\{10(x+y)=320}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=50}\\{6x+y=320}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=50}\\{6x+10y=320}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=50}\\{10x+6y=320}\end{array}\right.$ |
 已知,△ABC在平面直角坐标系中的位置如图所示.
已知,△ABC在平面直角坐标系中的位置如图所示.
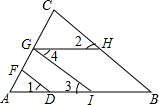 已知:如图,∠1=∠2,∠3=∠4,试说明DF∥BC.
已知:如图,∠1=∠2,∠3=∠4,试说明DF∥BC.