题目内容
17.已知二次函数y=ax2+bx+16的图象经过点(-2,40)和点(6,-8)(1)分别求a、b的值,并指出二次函数图象的顶点、对称轴;
(2)当-2≤x≤6时,试求二次函数y的最大值与最小值.
分析 (1)待定系数法可求得a、b的值,配方成二次函数顶点式可得顶点坐标、对称轴;
(2)由(1)知y=(x-5)2-9且-2≤x≤6,利用二次函数性质可得最值.
解答 解:(1)根据题意,将点(-2,40)和点(6,-8)代入y=ax2+bx+16,
得:$\left\{\begin{array}{l}{4a-2b+16=40}\\{36a+6b+16=-8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-10}\end{array}\right.$,
∴二次函数解析式为:y=x2-10x+16=(x-5)2-9,
该二次函数图象的顶点坐标为:(5,-9),对称轴为x=5;
(2)由(1)知当x=5时,y取得最小值-9,
在-2≤x≤6中,当x=-2时,y取得最大值40,
∴最大值y=40,最小值y=-9.
点评 本题考查了二次函数的性质及二次函数的最值,配方成顶点式是根本,熟练掌握二次函数的图象与性质是关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
2.体育测试时,一名九年级的学生推铅球,已知铅球所经过的路线为抛物线y=-$\frac{1}{12}$x2+x+$\frac{7}{3}$(单位:米)的一部分,根据关系式回答,该同学的成绩是( )
| A. | $\frac{7}{3}$米 | B. | $\frac{16}{3}$米 | C. | 14米 | D. | 6米 |
9.在-2,3,0,1中,绝对值最小的数是( )
| A. | -2 | B. | -3 | C. | 0 | D. | 1 |
6.下列计算正确的是( )
| A. | (a2)3=a5 | B. | a2÷a2=0 | C. | (2a)2=2a2 | D. | a•a2=a3 |
7.下列计算正确的是( )
| A. | (-x3)2=-x6 | B. | x6-x4=x2 | C. | x9÷x3=x3 | D. | x2•x3=x5 |
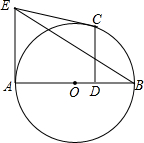 AB是的圆直径,从圆上一点C作CD⊥AB于D,圆在A,C两点的切线相交于E,证明:BE平分CD.
AB是的圆直径,从圆上一点C作CD⊥AB于D,圆在A,C两点的切线相交于E,证明:BE平分CD.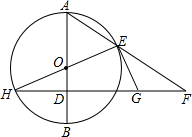 经过⊙O半径OB上一点D作直径AB的垂线交⊙O于点H,过直径HE的一端E作圆的切线交直线DH于G,延长AE交直线HD于点F.
经过⊙O半径OB上一点D作直径AB的垂线交⊙O于点H,过直径HE的一端E作圆的切线交直线DH于G,延长AE交直线HD于点F. 二次函数y=ax2+bx+c的图象如图所示,请你判断a,b,c及a+b+c的符号.
二次函数y=ax2+bx+c的图象如图所示,请你判断a,b,c及a+b+c的符号.