题目内容
8．
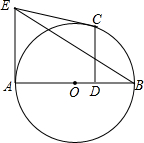AB是的圆直径，从圆上一点C作CD⊥AB于D，圆在A，C两点的切线相交于E，证明：BE平分CD．
分析 首先过B作圆的切线与EC延长线交于F，设CD与EB交于点H，进而得出$\frac{DH}{AE}$=$\frac{BH}{BE}$，$\frac{CH}{EC}$=$\frac{BF}{EF}$，进而得出$\frac{DH}{AE}$=$\frac{CH}{EC}$，即可得出答案．
解答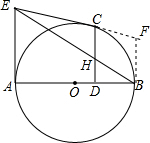 
解：过B作圆的切线与EC延长线交于F，设CD与EB交于点H，
则FC=FB，EA=EC，
∵AE∥CD∥BF，
∴$\frac{DH}{AE}$=$\frac{BH}{BE}$，$\frac{CH}{EC}$=$\frac{BF}{EF}$，
∵$\frac{BF}{EF}$=$\frac{FC}{EF}$=$\frac{BH}{EB}$，
∴$\frac{DH}{AE}$=$\frac{CH}{EC}$，
∴CH=DH，
∴BE平分CD．
点评 此题主要考查了切线的性质，根据题意正确应用平行线的性质是解题关键．
练习册系列答案
名师导航单元期末冲刺100分系列答案
相关题目
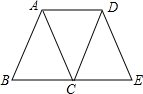如图，四边形ABCD是平行四边形，延长BC到点E，使CE=BC，你认为四边形ACED是平行四边形吗？请说明你的理由．
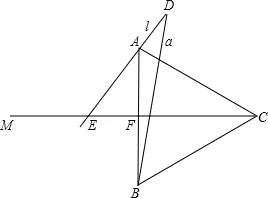如图所示，已知正△ABC中射线CM⊥AB于F，射线BA绕B顺时针旋转，旋转后的射线记作a，同时线段AB所在直线绕A顺时针旋转，旋转后的直线记作直线l，当直线l旋转的角度是射线a旋转角度的4倍时，直线l于射线CM相交于E，与射线a相交于D，且∠D=30°．
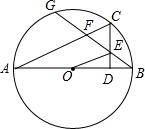如图，AB是⊙O的直径，C是$\widehat{BG}$的中点，CD⊥AB于D，BG交CD、AC与E、F．求证：