题目内容
6.若菱形的两条对角线长分别是12cm,16cm,则此菱形的边长是10cm,周长是40cm,面积是96cm2.分析 首先根据题意画出图形,由菱形两条对角线长分别是12cm和16cm,根据菱形的对角线互相垂直且平分,可求得OA与OB的值,再由勾股定理求得其边长,继而求得周长;然后根据菱形的面积等于对角线积的一半,即可求得其面积.
解答 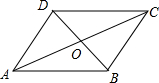 解:如图,∵四边形ABCD是菱形,AC=16cm,BD=12cm,
解:如图,∵四边形ABCD是菱形,AC=16cm,BD=12cm,
∴AC⊥BD,OA=$\frac{1}{2}$AC=8cm,OB=$\frac{1}{2}$BD=6cm,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=10cm,
∴它的周长为:40cm;
S菱形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×16×12=96(cm2).
故答案为:10cm,40cm,96cm2.
点评 此题考查了菱形的性质以及勾股定理.注意菱形的对角线互相平分且垂直,菱形的面积等于其对角线积的一半.

练习册系列答案
相关题目
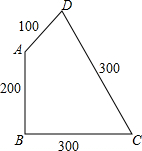 有一块薄铁片ABCD,∠B=90°,各边的尺寸如图所示(单位:cm),如果沿着对角线AC剪开,那么得到的两块三角形铁皮的形状都是“直角三角形”吗?请说明理由.
有一块薄铁片ABCD,∠B=90°,各边的尺寸如图所示(单位:cm),如果沿着对角线AC剪开,那么得到的两块三角形铁皮的形状都是“直角三角形”吗?请说明理由. 如图,四边形ABCD中,点E、G、F、H分别是边AD、BC和对角线BD、AC的中点,则四边形EFGH的形状是平行四边形
如图,四边形ABCD中,点E、G、F、H分别是边AD、BC和对角线BD、AC的中点,则四边形EFGH的形状是平行四边形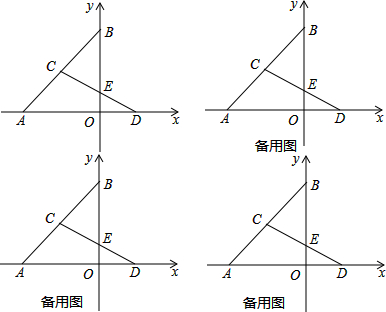
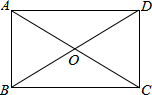 如图,矩形ABCD的两条对角线相交于点O,已知,AB=OA=3cm,求BD与AD的长.
如图,矩形ABCD的两条对角线相交于点O,已知,AB=OA=3cm,求BD与AD的长.
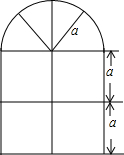 某窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长和半圆的半径均为acm.计算:
某窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长和半圆的半径均为acm.计算: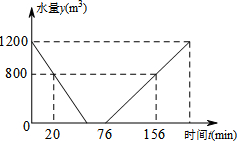 江阴水魔方游泳池常需进行换水清洗,途中的折线表示的是某个游泳池换水清洗过程“排水--清洗--灌水”中水量y(m3)与时间t(min)之间的函数关系式
江阴水魔方游泳池常需进行换水清洗,途中的折线表示的是某个游泳池换水清洗过程“排水--清洗--灌水”中水量y(m3)与时间t(min)之间的函数关系式