��Ŀ����
1����֪��ֱ��y=x+4��x�ᣬy��ֱ�A��B���㣮ֱ��y=kx-2k��x�ᡢy�ύ�ڵ�D��E�����߶�AB���ڵ�C��CΪAB���е㣮��1����k��ֵ��
��2������P�ӵ�A������ÿ��$\sqrt{2}$����λ���ȵ��ٶ����߶�AB�˶����յ�B�˶���ͬʱ������Q�ӵ�A������ÿ��2����λ���ȵ��ٶ������߶�AOB���յ�B�˶������PQE�����ΪS����P���˶�ʱ��Ϊt�룬��S��t�ĺ�����ϵʽ��ֱ��д��t��ȡֵ����
��3����P��Q���˶������У��Ƿ����ʱ��t��ʹtan��PEQ=$\frac{1}{2}$��
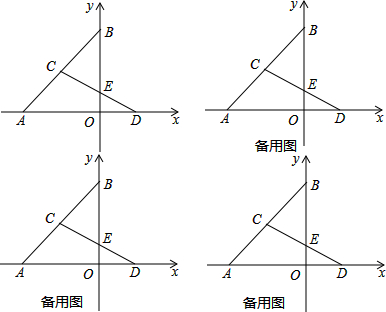
���� ��1������õ�B������Ϊ��0��4����A������Ϊ��-4��0�����Ӷ�����õ�C���е�����Ϊ��-2��2��������-2��2������y=kx-2k�����k��ֵ��
��2������ͼ1��ʾ������P��PF��OA������ΪF������SPEQ=S��ABO-S��APQ-S��QEO-S��PEB��⼴�ɣ�����ͼ2��ʾ������P��PF��OB������ΪF���������֪PF=4-t��QE=AO+OE-2t=5-2t��Ȼ�����������ε������ʽ��֪S��PQE=${t}^{2}-\frac{13}{2}t+10$������ͼ3��ʾ������P��PF��OB������ΪF����PF=4-t��QE=2t-5��Ȼ�����������ε������ʽ��⼴�ɣ�
��3����ͼ4��ʾ������E��EP��OA����AB�ڵ�P������P��PG��OA����ֱ��CD�Ľ���ʽΪy=-$\frac{1}{2}x+1$����֪tan��CDA=$\frac{1}{2}$��Ȼ��֤����CEP=��PEQ=��CDA���ɣ���ͼ5��ʾ������Q��EB��ʱ������P��PF��EB���������֪FB=PF=$\frac{\sqrt{2}}{2}PB$����tan��PEF=$\frac{1}{2}$��֪EF=2PF���Ӷ��õ�3BF=BE=3���������BF=1���ʴ�PB=$\sqrt{2}$��AP=3$\sqrt{3}$���Ӷ������t=3��
��� �⣺��1���߽�x=0����y=x+4�ã�y=4��
���B��������0��4����
�߽�y=0����y=x+4�ã�x+4=0����ã�x=-4��
���A��������-4��0����
�ߵ�C��A��B���е㣬
���C���е�����Ϊ��-2��2����
����-2��2������y=kx-2k�ã�-2k-2k=2��
��ã�k=-$\frac{1}{2}$��
��2����k=-$\frac{1}{2}$����y=kx-2k�ã�y=-$\frac{1}{2}x+1$��
�߽�x=0����ã�y=1��
���E��������0��1����
��OA=OB��
���BAO=��ABO=45�㣮
����ͼ1��ʾ������P��PF��OA������ΪF��
�ߡ�PAF=45�㣬
��PF=AF=$\frac{\sqrt{2}}{2}��\sqrt{2}t$=t��
��SPEQ=S��ABO-S��APQ-S��QEO-S��PEB
=$\frac{1}{2}��4��4$-$\frac{1}{2}��2t•t$-$\frac{1}{2}����4-2t����1$-$\frac{1}{2}��3����4-t��$
=-${t}^{2}+\frac{5}{2}t$��0��t��2����
����ͼ2��ʾ������P��PF��OB������ΪF��
��Rt��AOB��AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=4$\sqrt{2}$��
��PB=AB-AP��
��PB=4$\sqrt{2}$-$\sqrt{2}$t��
��PF=4-t��
�������֪��QE=AO+OE-2t=5-2t��
��S��PQE=$\frac{1}{2}����5-2t����4-t��$=${t}^{2}-\frac{13}{2}t+10$����2��t��2.5��
����ͼ3��ʾ������P��PF��OB������ΪF��
��PF=4-t��QE=2t-5��
��${S}_{��PQE}=\frac{1}{2}����2t-5������4-t��$=$-{t}^{2}+\frac{13}{2}t-10$����2.5��t��4����
����������S��t�ĺ�����ϵʽΪS=$\left\{\begin{array}{l}{-{t}^{2}+\frac{5}{2}t��0��t��2��}\\{{t}^{2}-\frac{13}{2}t+10��2��t��2.5��}\\{-{t}^{2}+\frac{13}{2}t-10��2.5��t��4��}\end{array}\right.$��
��3����ͼ4��ʾ������E��EP��OA����AB�ڵ�P������P��PG��OA��
��ֱ��CD�Ľ���ʽΪy=-$\frac{1}{2}x+1$��
��tan��CDA=$\frac{1}{2}$��
��EP��OA��PG��EO��OE=1��
��PG=1��
��AP=$\sqrt{2}$��
��t=1��
��t=1ʱ��AQ=2t=2��
���Q��������-2��0����
���C���Q����EP�Գƣ�
���CEP=��QEP��
��EP��AD��
���CEP=��CDA��
���PEQ=��CDA��
��tan��PEQ=$\frac{1}{2}$��
��ͼ5��ʾ������Q��EB��ʱ������P��PF��EB��
�ߡ�PBF=45�㣬��PFB=90�㣬
��FB=PF=$\frac{\sqrt{2}}{2}PB$��
��tan��PEF=$\frac{1}{2}$��
��EF=2PF��
��EF=2BF��
��3BF=BE=3��
��BF=1��
��PB=$\sqrt{2}$��
��AP=4$\sqrt{2}-\sqrt{2}$=3$\sqrt{3}$��
��t=3$\sqrt{2}$$��\sqrt{2}$=3��
������������t=1���t=3��ʱ��tan��PEQ=$\frac{1}{2}$��
���� ������Ҫ�������һ�κ������ۺ�Ӧ��������Ǻ���������ֱ�������ε����ʡ���Գ�ͼ�ε����ʡ�����ϵ������һ�κ����Ľ���ʽ�����ݸ���Լ������ε������ʽ���S��t�ĺ�����ϵʽ�ǽ���Ĺؼ���

 ÿ�α���ϵ�д�
ÿ�α���ϵ�д� ��ͼ��ʾ����������ABC�ı߳�Ϊ2��$\frac{AE}{BE}$=2��$\frac{AD}{DC}$=$\frac{1}{2}$��BD��CE�ڵ�F�����AEF�����Բ�뾶��Ϊ$\frac{2}{3}$��
��ͼ��ʾ����������ABC�ı߳�Ϊ2��$\frac{AE}{BE}$=2��$\frac{AD}{DC}$=$\frac{1}{2}$��BD��CE�ڵ�F�����AEF�����Բ�뾶��Ϊ$\frac{2}{3}$��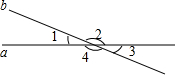 ��ͼ��ֱ��a��b�ཻ����1����2=2��7������ǵĶ�����
��ͼ��ֱ��a��b�ཻ����1����2=2��7������ǵĶ�����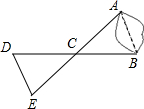 ��ͼ��A��B����ֱ�λ��һ�����������࣬����������һ��ˮ��D����BD���е�C����һ�ð��������С����A��������ֱ��ACһֱ��ǰ������C�ߵ���E��A��C��E������ͬһ��ֱ���ϣ�����ʹCE=CA��Ȼ����������E��ˮ��D�ľ��룬��DE�ij��Ⱦ���A��B����֮��ľ��룮
��ͼ��A��B����ֱ�λ��һ�����������࣬����������һ��ˮ��D����BD���е�C����һ�ð��������С����A��������ֱ��ACһֱ��ǰ������C�ߵ���E��A��C��E������ͬһ��ֱ���ϣ�����ʹCE=CA��Ȼ����������E��ˮ��D�ľ��룬��DE�ij��Ⱦ���A��B����֮��ľ��룮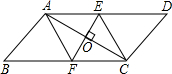 ��?ABCD�У��Խ���AC�Ĵ�ֱƽ���߷ֱ���AD��BC�ཻ�ڵ�E��F����AC���ڵ�O����֤���ı���AECF�����Σ�
��?ABCD�У��Խ���AC�Ĵ�ֱƽ���߷ֱ���AD��BC�ཻ�ڵ�E��F����AC���ڵ�O����֤���ı���AECF�����Σ�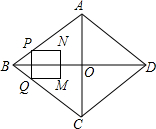 ��ͼ��������ABCD�У�AB=5cm��AC=6cm���Խ���AC��BD�ཻ�ڵ�O������P�ӵ�B������������BA-AD��1cm/s���ٶ����յ�D�˶�������P��PQ��AC������BC-CD�ڵ�Q����PQΪ����������PQMN����MN��ACʼ����PQ��ͬ�࣮��������PQMN���ABC�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����
��ͼ��������ABCD�У�AB=5cm��AC=6cm���Խ���AC��BD�ཻ�ڵ�O������P�ӵ�B������������BA-AD��1cm/s���ٶ����յ�D�˶�������P��PQ��AC������BC-CD�ڵ�Q����PQΪ����������PQMN����MN��ACʼ����PQ��ͬ�࣮��������PQMN���ABC�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����