Question

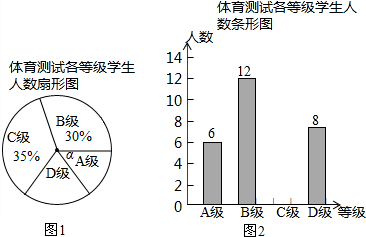
10．寒假期间，一些同学将要到A，B，C，D四个地方参加冬令营活动，现从这些同学中随机调查了一部分同学．根据调查结果，绘制成了如下两幅统计图：
（1）扇形A的圆心角的度数为108°，若此次冬令营一共有320名学生参加，则前往C地的学生约有64人，并将条形统计图补充完整；
（2）若某姐弟两人中只能有一人参加，姐弟俩决定用一个游戏来确定参加者：在4张形状、大小完全相同的卡片上分别写上-1，1，2，3四个整数，先让姐姐随机地抽取一张，再由弟弟从余下的三张卡片中随机地抽取一张．若抽取的两张卡片上的数字之和小于3则姐姐参加，否则弟弟参加．用列表法或树状图分析这种方法对姐弟俩是否公平？

Answer 1

分析 （1）根据两个统计图中的数据求出调查的总人数，进而确定出A的圆心角度数，利用样本与总体之间的关系求出C的学生数，补全条形统计图即可；
（2）列表得出所有等可能的情况数，找出数字之和小于3与数字之和大于等于3的情况数，求出姐弟两人参加的概率，比较即可得到结果．

解答 解：（1）由题意得：（30+20+10）÷（1-40%）=100（人），
则扇形A的圆心角的度数为$\frac{30}{100}$×360°=108°；
此次冬令营一共有320名学生参加，则前往C地的学生约有：$\frac{20}{100}$×320=64（人）；
B营地的人数是：100×40%=40（人），
补全条形统计图，如图所示；

故答案为：108；64；

（2）根据题意列表如下：

	-1	1	2	3
-1	---	（1，-1）	（2，-1）	（3，-1）
1	（-1，1）	---	（2，1）	（3，1）
2	（-1，2）	（1，2）	---	（3，2）
3	（-1，3）	（1，3）	（2，3）	---

所有等可能的情况有12种，其中抽取的两张卡片上的数字之和小于3的情况有6种，
∴P（数字之和小于3）=P（数字之和大于等于3）=$\frac{6}{12}$=$\frac{1}{2}$，
则此游戏公平．

点评 此题考查了游戏得公平性，判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．用到的知识点为：概率=所求情况数与总情况数之比．