题目内容
19.已知反比例函数y=$\frac{k-2}{x}$,在每一象限内,y随x增大而减小,则k的值可为3(答案不唯一)(写出满足条件的一个k的值即可)分析 根据反比例函数的性质,由在每一象限内y随x的增大而减小得到k-2>0,求出即可.
解答 解:∵反比例函数y=$\frac{k-2}{x}$在每一象限内,y随x的增大而减小,
∴k-2>0,
∴k>2.
故答案为3(答案不唯一).
点评 本题主要考查对反比例函数的性质,解一元一次不等式等知识点的理解和掌握,掌握当k>0,双曲线y=$\frac{k}{x}$的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列各数中一定是用科学记数法表示的为( )
| A. | 15×105 | B. | 0.03×105 | C. | a×107 | D. | 1.56×108 |
11.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{2}$×$\sqrt{8}$=4 | C. | $\sqrt{6}$÷$\sqrt{5}$=$\frac{\sqrt{6}}{5}$ | D. | $\sqrt{(-3)^{2}}$=-3 |
 已知如图为一几何体从不同方向看到的图形.
已知如图为一几何体从不同方向看到的图形.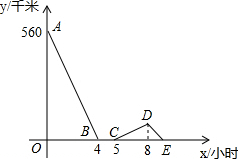 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题: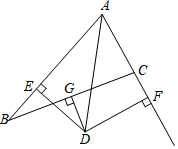 如图,在△ABC中,AB=7,AC=3,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F,下列说法正确的是( )
如图,在△ABC中,AB=7,AC=3,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F,下列说法正确的是( )