题目内容
6．已知，如图，AB与CD交于点O．（1）如图1，若AC∥BD，求证：∠A+∠C=∠B+∠D；
（2）如图2，若AC不平行BD，（1）中的结论是否仍然成立？请判断并证明你的结论．
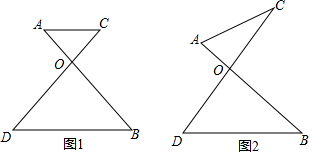
分析 （1）根据两直线平行，同位角相等证明；
（2）作AH∥BD交CD于H，根据平行线的性质和三角形的外角的性质证明．
解答 证明：（1）∵AC∥BD，
∴∠A=∠B，∠C=∠D，
∴∠A+∠C=∠B+∠D；
（2）（1）中的结论仍然成立．
作AH∥BD交CD于H，
由（1）得，∠OAH+∠OHA=∠B+∠D，
由三角形的外角的性质得，∠OHA=∠HAC+∠C，
∴∠OAH+∠HAC+∠C=∠B+∠D，
即∠OAC+∠C=∠B+∠D．
点评 本题考查的是平行线的性质、三角形的外角的性质，掌握三角形的一个外角等于与它不相邻的两个内角之和是解题的关键．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
17．请借鉴以前研究函数的经验，探索函数y=$\frac{6}{x-1}$+2的图象和性质．
（1）自变量x的取值范围为x≠1；
（2）填写下表，画出函数的图象；
（3）观察图象，写出该函数两条不同类型的性质；
（4）若x＞3，则y的取值范围为2＜y＜5；若y＜-1，则x的取值范围为-1＜x＜1．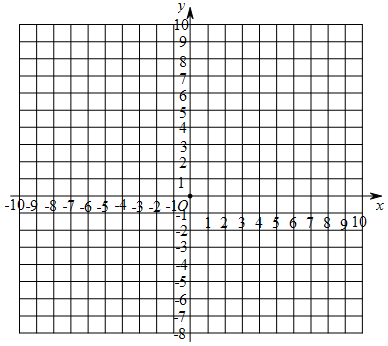
（1）自变量x的取值范围为x≠1；
（2）填写下表，画出函数的图象；
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| y | … | 1 | 0.8 | 0.5 | -1 | -4 | 8 |
（4）若x＞3，则y的取值范围为2＜y＜5；若y＜-1，则x的取值范围为-1＜x＜1．
已知如图为一几何体从不同方向看到的图形．
11．下列计算正确的是（ ）
| A． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B． | $\sqrt{2}$×$\sqrt{8}$=4 | C． | $\sqrt{6}$÷$\sqrt{5}$=$\frac{\sqrt{6}}{5}$ | D． | $\sqrt{（-3）^{2}}$=-3 |