题目内容
 如图,在△ABC中,∠C=90°,DE垂直平分AB,交AB于点E,交BC于点D,∠1=
如图,在△ABC中,∠C=90°,DE垂直平分AB,交AB于点E,交BC于点D,∠1=| 1 |
| 2 |
考点:线段垂直平分线的性质
专题:
分析:由DE垂直平分AB,根据线段垂直平分线的性质,可求得AD=BD,继而可得∠2=∠B,然后由在△ABC中,∠C=90°,∠1=
∠2,即可得∠BAC+∠B=
∠B=90°,继而求得答案.
| 1 |
| 2 |
| 5 |
| 2 |
解答:解:DE垂直平分AB,
∴AD=BD,
∴∠2=∠B,
∵∠1=
∠2,
∴∠1=
∠B,
∴∠BAC=∠1+∠2=
∠B,
∵在△ABC中,∠C=90°,
∴∠BAC+∠B=
∠B=90°,
∴∠B=36°.
∴AD=BD,
∴∠2=∠B,
∵∠1=
| 1 |
| 2 |
∴∠1=
| 1 |
| 2 |
∴∠BAC=∠1+∠2=
| 3 |
| 2 |
∵在△ABC中,∠C=90°,
∴∠BAC+∠B=
| 5 |
| 2 |
∴∠B=36°.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
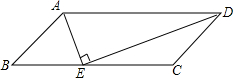 如图,?ABCD中,AE平分∠BAD,交BC于E,DE⊥AE,下列结论:①DE平分∠ADC;②E是BC的中点;③AD=2CD;④梯形ADCE的面积与△ABE的面积比是3:1,其中正确的个数是( )
如图,?ABCD中,AE平分∠BAD,交BC于E,DE⊥AE,下列结论:①DE平分∠ADC;②E是BC的中点;③AD=2CD;④梯形ADCE的面积与△ABE的面积比是3:1,其中正确的个数是( ) 如图,在?ABCD中,CE平分∠BCD交AB于E,DF平分∠ADC交AB于F,若AB=6,BC=4,求EF的长.
如图,在?ABCD中,CE平分∠BCD交AB于E,DF平分∠ADC交AB于F,若AB=6,BC=4,求EF的长. 如图所示,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,∠EDC+∠DCE=90°,试说明AD∥BC.
如图所示,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,∠EDC+∠DCE=90°,试说明AD∥BC. 如图,小明用量角器测得∠1=45°.∠2=45°,∠3=135°,你能判断哪些直线平行吗?为什么?
如图,小明用量角器测得∠1=45°.∠2=45°,∠3=135°,你能判断哪些直线平行吗?为什么? 已知:如图
已知:如图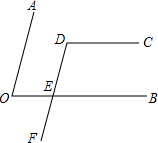 如图,∠AOE+∠BEF=180°,∠AOE+∠CDE=180°.请判断CD与BE是否平行,并说明理由.
如图,∠AOE+∠BEF=180°,∠AOE+∠CDE=180°.请判断CD与BE是否平行,并说明理由. 如图,平行于y轴的直尺(一部分)与双曲线y=
如图,平行于y轴的直尺(一部分)与双曲线y=