题目内容
 如图所示,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,∠EDC+∠DCE=90°,试说明AD∥BC.
如图所示,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,∠EDC+∠DCE=90°,试说明AD∥BC.考点:平行线的判定
专题:
分析:由条件和角平分线的定义可得到∠ADC+∠BCD=180°,可判定AD∥BC.
解答:证明:
∵CE平分∠BCD,DE平分∠ADC,
∴∠ADC=2∠EDC,∠BCD=2∠DCE,
∵∠EDC+∠DCE=90°,
∴2∠EDC+2∠DCE=180°,
即∠ADC+∠BCD=180°,
∴AD∥BC.
∵CE平分∠BCD,DE平分∠ADC,
∴∠ADC=2∠EDC,∠BCD=2∠DCE,
∵∠EDC+∠DCE=90°,
∴2∠EDC+2∠DCE=180°,
即∠ADC+∠BCD=180°,
∴AD∥BC.
点评:本题主要考查平行线的判定,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
下列语句,不是命题的是( )
| A、两点之间线段最短 |
| B、两直线不平行就相交 |
| C、连接A、B两点 |
| D、对顶角相等 |
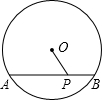 如图,AB是⊙O的弦,P是线段AB上一动点,OP长度满足2≤OP≤3,则AB=
如图,AB是⊙O的弦,P是线段AB上一动点,OP长度满足2≤OP≤3,则AB=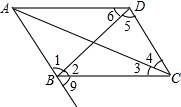 如图,若∠2=∠6,则
如图,若∠2=∠6,则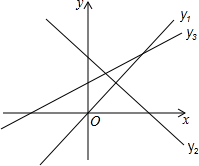 如图,已知直线y1=x,y2=-x+2,y3=
如图,已知直线y1=x,y2=-x+2,y3= 请你试用a,b,c,d表示如图所示的阴影部分的面积S,并求出当a=3,b=5,c=
请你试用a,b,c,d表示如图所示的阴影部分的面积S,并求出当a=3,b=5,c= 如图,在△ABC中,∠C=90°,DE垂直平分AB,交AB于点E,交BC于点D,∠1=
如图,在△ABC中,∠C=90°,DE垂直平分AB,交AB于点E,交BC于点D,∠1= 如图,已知∠1与∠2互补,∠1与∠3相等,那么AB和CD平行吗?EF和CH平行吗?说明理由.
如图,已知∠1与∠2互补,∠1与∠3相等,那么AB和CD平行吗?EF和CH平行吗?说明理由.