题目内容
若
=
=0解为负数,则m的取值范围为 .若
=
=0无解,m= .若
=
=0有增根,m= .
| m |
| x-4 |
| 1-x |
| 4-x |
| m |
| x-4 |
| 1-x |
| 4-x |
| m |
| x-4 |
| 1-x |
| 4-x |
考点:分式方程的解,分式方程的增根
专题:
分析:先解关于x的分式方程,求得x的值,然后再依据“解是负数”建立不等式求m的取值范围;分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.
解答:解:去分母,得m=x-1,
解得x=m+1,
∵x<0,
∴m+1<0,
解得m<-1;
∵
=
=0无解,
∴m+1=4,
∴m=3;
∵
=
=0有增根,
∴m+1=4,
∴m=3;
故答案为m<-1;3;3.
解得x=m+1,
∵x<0,
∴m+1<0,
解得m<-1;
∵
| m |
| x-4 |
| 1-x |
| 4-x |
∴m+1=4,
∴m=3;
∵
| m |
| x-4 |
| 1-x |
| 4-x |
∴m+1=4,
∴m=3;
故答案为m<-1;3;3.
点评:本题考查了分式方程的解,分式方程的增根以及分式方程无解的条件,是需要识记的内容.

练习册系列答案
相关题目
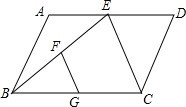 如图,?ABCD中,点E是AD边上的一个动点,FG是△BCE的中位线,在点E从A运动到D的过程中,FG与△BCE的面积变化分别为( )
如图,?ABCD中,点E是AD边上的一个动点,FG是△BCE的中位线,在点E从A运动到D的过程中,FG与△BCE的面积变化分别为( )| A、FG的长度不变,△BCE的面积也不改变 |
| B、FG的长度逐渐变大,△BCE的面积逐渐减小 |
| C、FG的长度先变大再变小,△BCE的面积逐渐变大 |
| D、FG的长度先变小再变大,△BCE的面积不改变 |
 如图,AC平分∠BCD,且∠BCA=∠CAD=
如图,AC平分∠BCD,且∠BCA=∠CAD=| 1 |
| 2 |
| A、36° | B、35° |
| C、37.5° | D、70° |
 如图,已知线段AB=2BC,DA=AB,M是线段AD的中点,N是线段AC的中点,试确定MN与AB+NB的大小关系.
如图,已知线段AB=2BC,DA=AB,M是线段AD的中点,N是线段AC的中点,试确定MN与AB+NB的大小关系. 一个物体的主视图如图所示,请你画出这个物体的俯视图(要求分别画出三种不同的情形)
一个物体的主视图如图所示,请你画出这个物体的俯视图(要求分别画出三种不同的情形)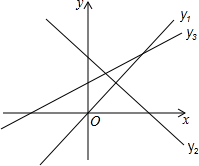 如图,已知直线y1=x,y2=-x+2,y3=
如图,已知直线y1=x,y2=-x+2,y3= 一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和地面是否垂直,为什么?
一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和地面是否垂直,为什么? 如图,在△ABC中,∠C=90°,DE垂直平分AB,交AB于点E,交BC于点D,∠1=
如图,在△ABC中,∠C=90°,DE垂直平分AB,交AB于点E,交BC于点D,∠1= 如图,已知∠1=∠2,AC平分∠DAB,则哪两条直线平行?说明理由.
如图,已知∠1=∠2,AC平分∠DAB,则哪两条直线平行?说明理由.