题目内容
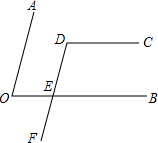 如图,∠AOE+∠BEF=180°,∠AOE+∠CDE=180°.请判断CD与BE是否平行,并说明理由.
如图,∠AOE+∠BEF=180°,∠AOE+∠CDE=180°.请判断CD与BE是否平行,并说明理由.考点:平行线的判定与性质
专题:
分析:由条件可得到∠BEF=∠CDE,可证明BE∥CD.
解答:解:平行,理由如下:
∵∠AOE+∠BEF=180°,∠AOE+∠CDE=180°,
∴∠BEF=∠CDE,
∴BE∥CD.
∵∠AOE+∠BEF=180°,∠AOE+∠CDE=180°,
∴∠BEF=∠CDE,
∴BE∥CD.
点评:本题主要考查平行线的性质和判定,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
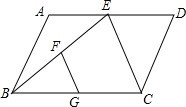 如图,?ABCD中,点E是AD边上的一个动点,FG是△BCE的中位线,在点E从A运动到D的过程中,FG与△BCE的面积变化分别为( )
如图,?ABCD中,点E是AD边上的一个动点,FG是△BCE的中位线,在点E从A运动到D的过程中,FG与△BCE的面积变化分别为( )| A、FG的长度不变,△BCE的面积也不改变 |
| B、FG的长度逐渐变大,△BCE的面积逐渐减小 |
| C、FG的长度先变大再变小,△BCE的面积逐渐变大 |
| D、FG的长度先变小再变大,△BCE的面积不改变 |
 如图,AC平分∠BCD,且∠BCA=∠CAD=
如图,AC平分∠BCD,且∠BCA=∠CAD=| 1 |
| 2 |
| A、36° | B、35° |
| C、37.5° | D、70° |
 如图,在△ABC中,∠C=90°,DE垂直平分AB,交AB于点E,交BC于点D,∠1=
如图,在△ABC中,∠C=90°,DE垂直平分AB,交AB于点E,交BC于点D,∠1= 如图,已知∠1=∠2,AC平分∠DAB,则哪两条直线平行?说明理由.
如图,已知∠1=∠2,AC平分∠DAB,则哪两条直线平行?说明理由.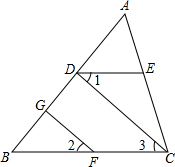 如图所示,已知∠ADE=∠B,∠1=∠2,GF⊥AB,求证:CD⊥AB.
如图所示,已知∠ADE=∠B,∠1=∠2,GF⊥AB,求证:CD⊥AB. 如图,已知线段AB平移后的位置点C,作出线段AB平移后的图形.
如图,已知线段AB平移后的位置点C,作出线段AB平移后的图形.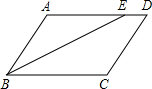 在?ABCD中,AB=6cm,AD=8cm,BE平分∠ABC,求DE的长度.
在?ABCD中,AB=6cm,AD=8cm,BE平分∠ABC,求DE的长度.