题目内容
1.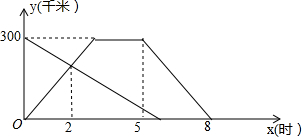 甲、乙两车分别从A、B两地同时出发相向而行,并以各自的速度匀速行驶,甲车到达B地后,停留一段时间,然后按原路原速度返回A地;乙车到达A地立即停止行驶.甲、乙两车和A地的距离y(千米)与甲车出发时间x(时)的函数图象如图所示.
甲、乙两车分别从A、B两地同时出发相向而行,并以各自的速度匀速行驶,甲车到达B地后,停留一段时间,然后按原路原速度返回A地;乙车到达A地立即停止行驶.甲、乙两车和A地的距离y(千米)与甲车出发时间x(时)的函数图象如图所示.(1)求甲、乙两车的速度.
(2)甲车的停留时间是2小时.
(3)求甲车从B地返回到A地的过程中,y与x之间的函数关系式.
(4)当两车相距100千米时,x的值为$\frac{4}{3},\frac{8}{3}$,7.
分析 (1)根据函数图象可以分别求得甲、乙两车的速度;
(2)根据函数图象可以求得甲车停留的时间;
(3)根据函数图象可以求得甲车从B地返回到A地的过程中,y与x之间的函数关系式;
(4)根据函数图象可以求得甲车各段的函数解析式,从而可以求得两车相距100千米时的x的值.
解答 解:(1)由图可得,
甲车的速度:300÷(8-5)=100(千米/小时),
乙车的速度:(300-100×2)÷2=50(千米/小时),
即甲车的速度是100千米/时,乙车的速度是50千米/时;
(2)由图可得,
甲车的停留时间是:5-(8-5)=2(小时),
故答案为:2;
(3)设甲车从B地返回到A地的过程中,y与x之间的函数关系式为y=kx+b.
将(5,300),(8,0)代入可得,
$\left\{\begin{array}{l}{5k+b=300}\\{8k+b=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-100}\\{b=800}\end{array}\right.$,
即甲车从B地返回到A地的过程中,y与x之间的函数关系式是y=-100x+800(5≤x≤8);
(4)设甲车从A到B地对应的解析式为y=ax,
则300=3a,得a=100,
∴y=100x(0≤x≤3),
设乙车从B地到A地对应的函数解析式为y=mx+n,
则$\left\{\begin{array}{l}{n=300}\\{6m+n=0}\end{array}\right.$,得$\left\{\begin{array}{l}{m=-50}\\{n=300}\end{array}\right.$,
∴乙车从B地到A地对应的函数解析式为y=-50x+300,
则|-50x+300-100x|=100,
解得,x1=$\frac{4}{3}$,x2=$\frac{8}{3}$,
将y=100代入y=-100x+800,得x=7,
故答案为:$\frac{4}{3},\frac{8}{3}$,7.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


| A. | 6 | B. | -8 | C. | 8 | D. | -6 |
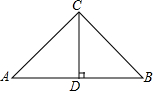 如图:在等腰直角△ABC中,CA=CB,CD⊥AB于D,AB=10,则CD=5.
如图:在等腰直角△ABC中,CA=CB,CD⊥AB于D,AB=10,则CD=5. 如图,△ABC中,∠A=25°,∠B=70°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,则∠EDF=22.5°.
如图,△ABC中,∠A=25°,∠B=70°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,则∠EDF=22.5°. 实数a、b在数轴上的位置如图所示,则化简|a+2b|-|a-b|的结果为2a+b.
实数a、b在数轴上的位置如图所示,则化简|a+2b|-|a-b|的结果为2a+b. 一个圆形零件的部分碎片如图所示.请你利用尺规作图找到圆心O.(要求:不写作法,保留作图痕迹)
一个圆形零件的部分碎片如图所示.请你利用尺规作图找到圆心O.(要求:不写作法,保留作图痕迹)