题目内容
16.已知a+b=3,ab=1,则$\frac{a}{b}$+$\frac{b}{a}$的值等于7;已知(a+b)2=20,(a-b)2=4,则ab=4.
分析 将a+b=3,ab=1代入原式=$\frac{{a}^{2}+{b}^{2}}{ab}$=$\frac{(a+b)^{2}-2ab}{ab}$即可得;
由已知等式可得a2+2ab+b2=20 ①,${a}^{2}-2ab+{b}^{2}=4\\;\$ ②,①-②即可得.
解答 解:当a+b=3,ab=1时,
原式=$\frac{{a}^{2}+{b}^{2}}{ab}$
=$\frac{(a+b)^{2}-2ab}{ab}$
=$\frac{{3}^{2}-2}{1}$
=7;
∵(a+b)2=20,(a-b)2=4,
∴a2+2ab+b2=20 ①,
${a}^{2}-2ab+{b}^{2}=4\\;\$ ②,
①-②,得:4ab=16,
∴ab=4,
故答案为:7,4.
点评 本题主要考查分式的化简求值,熟练掌握完全平方公式是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
6.已知x=5是方程ax+4=16-a的解,则a的值是( )
| A. | -2 | B. | 2 | C. | 5 | D. | -5 |
4.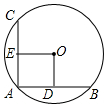 如图,在⊙O中,相等的弦AB、AC互相垂直,OE⊥AC于E,OD⊥AB于D,则四边形OEAD为( )
如图,在⊙O中,相等的弦AB、AC互相垂直,OE⊥AC于E,OD⊥AB于D,则四边形OEAD为( )
 如图,在⊙O中,相等的弦AB、AC互相垂直,OE⊥AC于E,OD⊥AB于D,则四边形OEAD为( )
如图,在⊙O中,相等的弦AB、AC互相垂直,OE⊥AC于E,OD⊥AB于D,则四边形OEAD为( )| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |
 如图是正方体的展开图,若约定用字母S表示正方体的侧面,用T表示上面,A表示底面,则字母A在展开图中的位置是( )
如图是正方体的展开图,若约定用字母S表示正方体的侧面,用T表示上面,A表示底面,则字母A在展开图中的位置是( )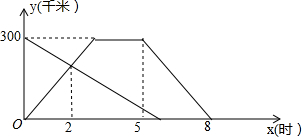 甲、乙两车分别从A、B两地同时出发相向而行,并以各自的速度匀速行驶,甲车到达B地后,停留一段时间,然后按原路原速度返回A地;乙车到达A地立即停止行驶.甲、乙两车和A地的距离y(千米)与甲车出发时间x(时)的函数图象如图所示.
甲、乙两车分别从A、B两地同时出发相向而行,并以各自的速度匀速行驶,甲车到达B地后,停留一段时间,然后按原路原速度返回A地;乙车到达A地立即停止行驶.甲、乙两车和A地的距离y(千米)与甲车出发时间x(时)的函数图象如图所示.