题目内容
11.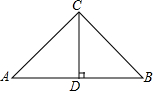 如图:在等腰直角△ABC中,CA=CB,CD⊥AB于D,AB=10,则CD=5.
如图:在等腰直角△ABC中,CA=CB,CD⊥AB于D,AB=10,则CD=5.
分析 由已知可得Rt△ABC是等腰直角三角形,得出AD=BD=$\frac{1}{2}$AB=5,再由直角三角形斜边的中线等于斜边的一半得出CD=BD=5.
解答 解:∵∠ACB=90°,CA=CB,
∴∠A=∠B=45°,
∵CD⊥AB,
∴AD=BD=$\frac{1}{2}$AB=5,∠CDB=90°,
∴CD=BD=5.
故答案为5
点评 本题主要考查了等腰直角三角形,解题的关键是灵活运用等腰直角三角形的性质求角及边的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.若单项式-2am+2b与5ab2m+n是同类项,则mn的值是( )
| A. | 1 | B. | -1 | C. | 16 | D. | -32 |
6.已知x=5是方程ax+4=16-a的解,则a的值是( )
| A. | -2 | B. | 2 | C. | 5 | D. | -5 |
20. AB为⊙O的直径,点C、D在⊙O上.若∠ABD=42°,则∠BCD的度数是( )
AB为⊙O的直径,点C、D在⊙O上.若∠ABD=42°,则∠BCD的度数是( )
 AB为⊙O的直径,点C、D在⊙O上.若∠ABD=42°,则∠BCD的度数是( )
AB为⊙O的直径,点C、D在⊙O上.若∠ABD=42°,则∠BCD的度数是( )| A. | 122° | B. | 132° | C. | 128° | D. | 138° |
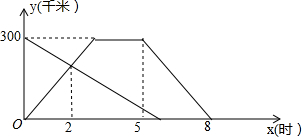 甲、乙两车分别从A、B两地同时出发相向而行,并以各自的速度匀速行驶,甲车到达B地后,停留一段时间,然后按原路原速度返回A地;乙车到达A地立即停止行驶.甲、乙两车和A地的距离y(千米)与甲车出发时间x(时)的函数图象如图所示.
甲、乙两车分别从A、B两地同时出发相向而行,并以各自的速度匀速行驶,甲车到达B地后,停留一段时间,然后按原路原速度返回A地;乙车到达A地立即停止行驶.甲、乙两车和A地的距离y(千米)与甲车出发时间x(时)的函数图象如图所示.