题目内容
2.在平面直角坐标系中,点A为(3,2),连接OA并把线段OA绕原点O逆时针旋转180°,所得到的对应点A′的坐标为( )| A. | (3,2) | B. | (2,-3) | C. | (-3,-2) | D. | (3,-2) |
分析 根据关于原点中心对称的点的坐标特征求解.
解答 解:∵线段OA绕原点O逆时针旋转180°,A点的对应点A′,
即点A与点A′关于原点中心对称,
∴A′点的坐标为(-3,-2).
故选C.
点评 本题考查了坐标与图形变化:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
7.实数π,0,$\sqrt{5}$,-6其中最大的数是( )
| A. | $\sqrt{5}$ | B. | π | C. | 0 | D. | -6 |
14.在四个实数-2,0,$-\sqrt{3}$,5中,最小的实数是( )
| A. | -2 | B. | 0 | C. | $-\sqrt{3}$ | D. | 5 |
11. 如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=600m,那么他实际上升的高度BC为( )
如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=600m,那么他实际上升的高度BC为( )
 如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=600m,那么他实际上升的高度BC为( )
如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=600m,那么他实际上升的高度BC为( )| A. | 300$\sqrt{3}$m | B. | 1200m | C. | 300m | D. | 200$\sqrt{3}$m |
9.若函数y=kx+b的函数值y随x的增大而减小,则函数y=(5-k)x的图象经过的象限是( )
| A. | 第一、三象限 | B. | 第一、二象限 | C. | 第二、四象限 | D. | 第三、四象限 |
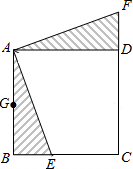 如图,在正方形ABCD中,E是BC上一点,△ABE经过旋转后得到△ADF.
如图,在正方形ABCD中,E是BC上一点,△ABE经过旋转后得到△ADF.
 如图.双曲线y=$\frac{k}{x}$与直线y=x-2相交于A、B两点,点A的纵坐标为1.
如图.双曲线y=$\frac{k}{x}$与直线y=x-2相交于A、B两点,点A的纵坐标为1.