题目内容
9.若函数y=kx+b的函数值y随x的增大而减小,则函数y=(5-k)x的图象经过的象限是( )| A. | 第一、三象限 | B. | 第一、二象限 | C. | 第二、四象限 | D. | 第三、四象限 |
分析 由函数y=kx+b为减函数可知k<0,由此可得出5-k>0,根据一次函数图象与系数的关系即可得出函数y=(5-k)x的图象经过的象限.
解答 解:∵函数y=kx+b的函数值y随x的增大而减小,
∴k<0,
∴5-k>5,
∴函数y=(5-k)x的图象经过第一、三象限.
故选A.
点评 本题考查了一次函数图象与系数的关系,解题的关键是找出5-k>0.本题属于基础题,难度不大,解决该题型题目时,根据k值结合一次函数图象与系数的关系,得出函数图象经过的象限是关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
2.在平面直角坐标系中,点A为(3,2),连接OA并把线段OA绕原点O逆时针旋转180°,所得到的对应点A′的坐标为( )
| A. | (3,2) | B. | (2,-3) | C. | (-3,-2) | D. | (3,-2) |
16.分别取正整数5的绝对值、倒数、相反数、算术平方根,得到的数值仍为正整数的是( )
| A. | 绝对值 | B. | 倒数 | C. | 相反数 | D. | 算术平方根 |
17.在$\sqrt{2}$,-1,-3,0这四个实数中,最小的是( )
| A. | $\sqrt{2}$ | B. | -1 | C. | -3 | D. | 0 |
 =
= 时,求DE的长.
时,求DE的长.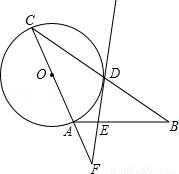
 如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=-1.
如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=-1.