题目内容
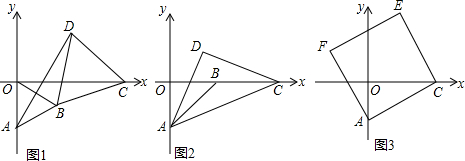
13.如图1,△ABC是边长为6的等边三角形,点D、E分别是边AB、AC的中点,将△ADE绕点A旋转,BD与CE所在的直线交于点F.(1)如图(2)所示,将△ADE绕点A逆时针旋转,且旋转角不大于60°,∠CFB的度数是多少?说明你的理由?
(2)当△ADE绕点A旋转时,若△BCF为直角三角形,线段BF的长为4$\sqrt{3}$或2$\sqrt{3}$(请直接写出答案)

分析 (1)根据等边三角形的性质得到AC=AB,∠EAD=∠CAB=60°,由点D、E分别是边AB、AC的中点,得到AE=AD,根据旋转的性质得到∠EAC=∠BAD,根据全等三角形的性质得到∠ACE=∠ABD,推出A,B,C,F四点共圆,根据圆周角定理即可得到结论;
(2)解直角三角形即可得到结论.
解答 解:(1)∠CFB=60°,
理由:∵△ABC是等边三角形,
∴AC=AB,∠EAD=∠CAB=60°,
∵点D、E分别是边AB、AC的中点,
∴AE=AD,
∵将△ADE绕点A旋转,BD与CE所在的直线交于点F,
∴∠EAC=∠BAD,
在△ACE与△ABD中,
$\left\{\begin{array}{l}{AE=AD}\\{∠EAC=∠DAB}\\{AC=AB}\end{array}\right.$,
∴△ACE≌△ABD,
∴∠ACE=∠ABD,
∴A,B,C,F四点共圆,
∴∠CFB=∠CAB=60°;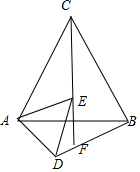
(2)∵∠CFB=60°,∠BCF=90°,
∴∠CBF=30°,
∴BF=$\frac{BC}{cos30°}$=$\frac{6}{\frac{\sqrt{3}}{2}}$=4$\sqrt{3}$.
∵∠CFB=60°,∠CBF=90°,
∴BF=$\frac{\sqrt{3}}{3}$BC=2$\sqrt{3}$.
故答案为:4$\sqrt{3}$或2$\sqrt{3}$.
点评 本题考查了旋转的性质,等边三角形的性质,解直角三角形,正确的理解题意是解题的关键.

练习册系列答案
相关题目
5.已知-4a5bm÷28anb2=-$\frac{1}{7}$b2,则m、n的值为( )
| A. | m=4,n=2 | B. | m=4,n=5 | C. | m=1,n=3 | D. | m=2,n=3 |
8.一组数据1,2,3,4,5的方差为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
18.圆锥的侧面展开图为半径为16,且圆心角为90°的扇形,则这个圆锥的底面半径为( )
| A. | 16 | B. | 4 | C. | 4$\sqrt{2}$ | D. | 8 |
5.下列命题正确的是( )
| A. | 一组对边相等,另一组对边平行的四边形是平行四边形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相垂直平分且相等的四边形是正方形 |
2.在平面直角坐标系中,点A为(3,2),连接OA并把线段OA绕原点O逆时针旋转180°,所得到的对应点A′的坐标为( )
| A. | (3,2) | B. | (2,-3) | C. | (-3,-2) | D. | (3,-2) |
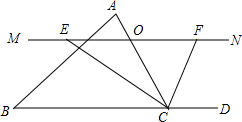 已知△ABC中,点O是边AC上的一个动点,过O做直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
已知△ABC中,点O是边AC上的一个动点,过O做直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.