题目内容
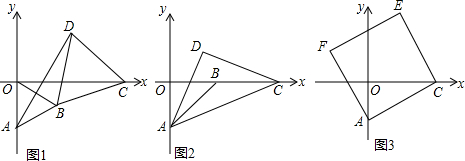
10. 如图.双曲线y=$\frac{k}{x}$与直线y=x-2相交于A、B两点,点A的纵坐标为1.
如图.双曲线y=$\frac{k}{x}$与直线y=x-2相交于A、B两点,点A的纵坐标为1.(1)①直接写出B点坐标:(-1,-3)
②双曲线上有两点C、D(A、D在双曲线的同-支上),使四边形ABCD为平行四边形,则C(-3,-1),D(1,3)(直接写出结果)
(2)直接写出关于x的不等式:x-2-$\frac{k}{x}$<0的解集.
分析 (1)由A点在直线上且纵坐标为1可得其坐标,根据A点坐标可得双曲线解析式,由直线及双曲线解析式联立方程组,解方程组可得两交点坐标;
(2)根据双曲线的中心对称性可知,点B关于原点的对称点即为点D、点A关于原点的对称点即为点C,此时C、D均在双曲线上且AC、BD互相平分,即四边形ABCD是平行四边形,据此可得点C、D的坐标;
(3)结合图象,不等式x-2-$\frac{k}{x}$<0的解就是对相同的x的值,反比例函数的图象在上边的部分,对应的x的范围.
解答 解:(1)∵点A的纵坐标为1,
∴将y=1代入y=x-2,得:1=x-2,解得:x=3,
则点A的坐标为(3,1),
将点A(3,1)代入y=$\frac{k}{x}$,得:k=3,
∴双曲线解析式为:y=$\frac{3}{x}$,
根据题意,$\left\{\begin{array}{l}{y=x-2}\\{y=\frac{3}{x}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$,
∴点B的坐标为(-1,-3);
(2)∵点A(3,1)关于原点的对称点(-3,-1)也在双曲线上,
点B(-1,-3)关于原点的对称点(1,3)在双曲线上,
∴当点C坐标为(-3,-1)、点D坐标为(1,3)时,四边形ABCD是平行四边形;
(3)观察图象可知,当x<-1或0<x<3时,x-2-$\frac{k}{x}$<0.
故答案为:(1)-1,-3;(2)-3,-1;1,3.
点评 本题考查了一次函数与反比例函数交点问题,待定系数法求函数解析式,联立两直线解析式求交点坐标的方法,求一次函数与一元一次不等式关键在于准确识图,确定出两函数图象的对应的函数值的大小.

| A. | x2-4 | B. | -x2-y2+2xy | C. | m2n2-1 | D. | a2-4b2 |
| A. | 16 | B. | 4 | C. | 4$\sqrt{2}$ | D. | 8 |
| A. | 一组对边相等,另一组对边平行的四边形是平行四边形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相垂直平分且相等的四边形是正方形 |
| A. | (3,2) | B. | (2,-3) | C. | (-3,-2) | D. | (3,-2) |
| A. | 1 | B. | -1 | C. | $\sqrt{2}$ | D. | 2 |
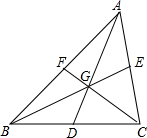 如图,△ABC的三条中线相交于点G.
如图,△ABC的三条中线相交于点G.