题目内容
17.已知抛物线y=x2+mx-$\frac{3}{4}$m2(m>0)与x轴交于A、B两点,设抛物线与y轴交于点C,若△ABC是直角三角形,则△ABC的面积为$\frac{2\sqrt{3}}{3}$.分析 由△ABC是直角三角形,推出OC2=OA•OB即可解决问题.
解答 解:令y=0,则x2+mx-$\frac{3}{4}$m2=0,解得x=-$\frac{3}{2}$m或$\frac{1}{2}$m,
不妨设点A坐标(-$\frac{3}{2}$m,0),点B坐标为($\frac{1}{2}$m,0),点C(0,-$\frac{3}{4}$m2),
∵△ABC都是直角三角形,
∴OC2=OA•OB,
∴$\frac{9}{16}$m4=$\frac{3}{4}$m2,
∴m=0或m=±$\frac{2\sqrt{3}}{3}$,
∵m>0,
∴m=$\frac{2\sqrt{3}}{3}$.
故答案为$\frac{2\sqrt{3}}{3}$.
点评 本题考查抛物线与x轴交点,射影定理等知识,解题的关键是利用射影定理列出方程,学会转化的思想解决问题,属于中考常考题型.

练习册系列答案
相关题目
8.下列计算错误的是( )
| A. | x•x5=x6 | B. | a6÷a2=a3 | C. | (ab2)3=a3b6 | D. | (-a2)2=a4 |
8.一组数据1,2,3,4,5的方差为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
5.下列命题正确的是( )
| A. | 一组对边相等,另一组对边平行的四边形是平行四边形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相垂直平分且相等的四边形是正方形 |
2.在平面直角坐标系中,点A为(3,2),连接OA并把线段OA绕原点O逆时针旋转180°,所得到的对应点A′的坐标为( )
| A. | (3,2) | B. | (2,-3) | C. | (-3,-2) | D. | (3,-2) |
9.下列运算中,正确的是( )
| A. | x3+x=x4 | B. | (x2)3=x6 | C. | 3x-2x=-1 | D. | (a-b)2=a2-b2 |
6.不等式2x-2≤0的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
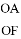 =
= 时,求DE的长.
时,求DE的长.