题目内容
18.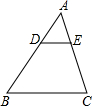 如图,在△ABC中,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,DE=4cm,则BC的长为( )
如图,在△ABC中,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,DE=4cm,则BC的长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 11cm |
分析 由DE∥BC,得到△ADE∽△ABC,得到比例式$\frac{AD}{AB}$=$\frac{DE}{BC}$,即可得到结果.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$,
∴$\frac{4}{BC}$=$\frac{1}{3}$,
∴BC=12.
故选C.
点评 本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.

练习册系列答案
相关题目
13.若a=$\frac{1}{\sqrt{2}}$,b=$\frac{\sqrt{2}}{2}$,则( )
| A. | a=b | B. | a、b互为倒数 | C. | ab=2 | D. | a、b互为相反数 |
10. 如图,在直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4,…,则点A2015的坐标是( )
如图,在直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4,…,则点A2015的坐标是( )
 如图,在直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4,…,则点A2015的坐标是( )
如图,在直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4,…,则点A2015的坐标是( )| A. | (-2015,-2015) | B. | (-504$\sqrt{2}$,-504$\sqrt{2}$) | C. | (-252$\sqrt{2}$,252$\sqrt{2}$) | D. | (-252$\sqrt{2}$,-252$\sqrt{2}$) |
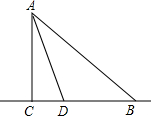 如图,在Rt△ACB中,∠ACB=90°,AC=BC=12,D为边BC上一点,CD=4,K为直线BC上一点,∠DAK=45°,则CK的长为24或6.
如图,在Rt△ACB中,∠ACB=90°,AC=BC=12,D为边BC上一点,CD=4,K为直线BC上一点,∠DAK=45°,则CK的长为24或6. 如图,在四边形ABCD中,AD、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.
如图,在四边形ABCD中,AD、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.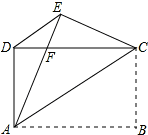 如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.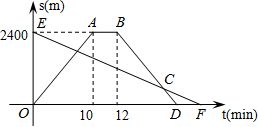 小明早8点从家骑自行车出发,沿一条直路去邮局办事,小明出发的同时,他的爸爸从邮局沿同一条道路步行回家,小明在邮局停留了一会后沿原路以原速度返回,小明比爸爸早3分钟到家.设他们与家的距离S(m)与离开家的时间t(min)之间函数关系的如图所示,有下列说法:①邮局与家的距离为2400米;②小明到家的时间为8:22分;③爸爸的速度为96mAmin;④小明在返回途中离家480米处于爸爸相遇,其中正确的说法有( )
小明早8点从家骑自行车出发,沿一条直路去邮局办事,小明出发的同时,他的爸爸从邮局沿同一条道路步行回家,小明在邮局停留了一会后沿原路以原速度返回,小明比爸爸早3分钟到家.设他们与家的距离S(m)与离开家的时间t(min)之间函数关系的如图所示,有下列说法:①邮局与家的距离为2400米;②小明到家的时间为8:22分;③爸爸的速度为96mAmin;④小明在返回途中离家480米处于爸爸相遇,其中正确的说法有( )