题目内容
12.若a2+2a-1=0,求:$\frac{1}{a+1}$-$\frac{a+3}{{a}^{2}-1}$•$\frac{{a}^{2}-2a+1}{{a}^{2}+4a+3}$的值.分析 原式第二项约分后,两项通分并利用同分母分式的减法法则计算,得到最简结果,把已知等式变形后代入计算即可求出值.
解答 解:原式=$\frac{1}{a+1}$-$\frac{a+3}{(a+1)(a-1)}$•$\frac{(a-1)^{2}}{(a+1)(a+3)}$=$\frac{1}{a+1}$-$\frac{a-1}{(a+1)^{2}}$=$\frac{a+1-a+1}{(a+1)^{2}}$=$\frac{2}{{a}^{2}+2a+1}$,
当a2+2a-1=0,即a2+2a=1时,原式=2.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
18.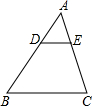 如图,在△ABC中,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,DE=4cm,则BC的长为( )
如图,在△ABC中,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,DE=4cm,则BC的长为( )
 如图,在△ABC中,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,DE=4cm,则BC的长为( )
如图,在△ABC中,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,DE=4cm,则BC的长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 11cm |
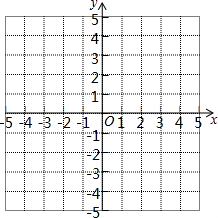 在如图的直角坐标系中,画出点A(-1,-1),B(3,-1),C(4,2),D(0,2),并将各点依次用线段连接起来,求图形ABCD的面积.(每个小方格的长和宽都为一个长度单位)
在如图的直角坐标系中,画出点A(-1,-1),B(3,-1),C(4,2),D(0,2),并将各点依次用线段连接起来,求图形ABCD的面积.(每个小方格的长和宽都为一个长度单位)