题目内容
3. 如图,在四边形ABCD中,AD、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.
如图,在四边形ABCD中,AD、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.(1)∠1与∠2相等吗?为什么?
(2)判断△ABE与△ACD是否相似?并说明理由.
分析 (1)由$\frac{AB}{AE}=\frac{BC}{ED}=\frac{AC}{AD}$,得到△ABC∽△AED,推出∠BAC=∠EAD,即可得到∠1=∠2;
(2)由$\frac{AB}{AE}=\frac{AC}{AD}$得$\frac{AB}{AC}=\frac{AE}{AD}$,根据两边对应成比例且夹角相等得到△ABE∽△ACD.
解答 解:(1)∠1与∠2相等.
在△ABC和△AED中,
∵$\frac{AB}{AE}=\frac{BC}{ED}=\frac{AC}{AD}$,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠1=∠2.
(2)△ABE与△ACD相似.
由$\frac{AB}{AE}=\frac{AC}{AD}$得$\frac{AB}{AC}=\frac{AE}{AD}$,
在△ABE和△ACD中,
∵$\frac{AB}{AC}=\frac{AE}{AD}$,∠1=∠2,
∴△ABE∽△ACD.
点评 本题考查了相似三角形的判定和性质,熟记定理是解题的关键.

练习册系列答案
相关题目
11.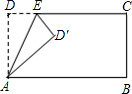 如图,将长方形ABCD沿AE折叠,已知∠AED=65°,则∠CED的大小是( )
如图,将长方形ABCD沿AE折叠,已知∠AED=65°,则∠CED的大小是( )
 如图,将长方形ABCD沿AE折叠,已知∠AED=65°,则∠CED的大小是( )
如图,将长方形ABCD沿AE折叠,已知∠AED=65°,则∠CED的大小是( )| A. | 50° | B. | 55° | C. | 65° | D. | 75° |
18.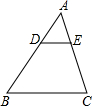 如图,在△ABC中,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,DE=4cm,则BC的长为( )
如图,在△ABC中,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,DE=4cm,则BC的长为( )
 如图,在△ABC中,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,DE=4cm,则BC的长为( )
如图,在△ABC中,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,DE=4cm,则BC的长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 11cm |
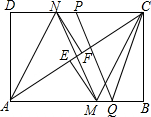 如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在对角线BC上的点E、F处,折痕分别为CM、AN.连接MF、NE. P、Q是矩形的边CD、AB上的两点,连结PQ、CQ、MN.若PQ=CQ,PQ∥MN,且AB=4,BC=3,则PC的长度是2.
如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在对角线BC上的点E、F处,折痕分别为CM、AN.连接MF、NE. P、Q是矩形的边CD、AB上的两点,连结PQ、CQ、MN.若PQ=CQ,PQ∥MN,且AB=4,BC=3,则PC的长度是2.