题目内容
7.计算下列各题:(1)$\sqrt{2}$(2cos45°-sin60°)+$\frac{\sqrt{24}}{4}$;
(2)(-2)0+3tan30°+|$\sqrt{3}$-2|.
分析 (1)利用特殊角的三角函数值代入化简,进而合并同类二次根式即可;
(2)利用特殊角的三角函数值以及绝对值的性质和零指数幂的性质化简求出即可.
解答 解:(1)$\sqrt{2}$(2cos45°-sin60°)+$\frac{\sqrt{24}}{4}$
=$\sqrt{2}$×(2×$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{2}$)+$\frac{\sqrt{6}}{2}$
=2;
(2)(-2)0+3tan30°+|$\sqrt{3}$-2|
=1+3×$\frac{\sqrt{3}}{3}$+2-$\sqrt{3}$
=3.
点评 此题主要考查了二次根式的混合运算以及特殊角的三角函数值,正确化简二次根式是解题关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
8.合肥市某商场为做好“家电下乡”的惠民服务,决定从厂家购进甲、乙、丙三种不同型号的电视机108台,其中甲种电视机的台数是丙种的4倍,购进三种电视机的总金额不超过147000元,已知甲、乙、丙三种型号的电视机的出厂价格和售出后每台的利润如下表:
(1)求该商场至少购买丙种电视机多少台?
(2)若要求甲种电视机的台数不超过乙种电视机的台数,且使售出后所获利润最高,请设计进货方案,并求出售出后的最高利润.
| 型号 | 甲 | 乙 | 丙 |
| 出厂价(元/台) | 1000 | 1500 | 2000 |
| 每台利润(元/台) | 200 | 200 | 300 |
(2)若要求甲种电视机的台数不超过乙种电视机的台数,且使售出后所获利润最高,请设计进货方案,并求出售出后的最高利润.
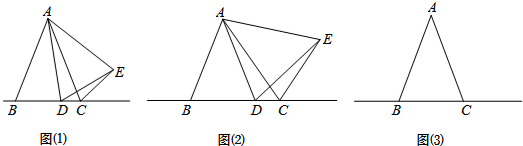
 如图,已知二次函数y=ax2+bx+c的图象与x轴交于点A、B,与y轴交于点C.
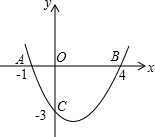
如图,已知二次函数y=ax2+bx+c的图象与x轴交于点A、B,与y轴交于点C. 已知:如图,DA=CB,∠ADC=∠BCD.求证:∠ADB=∠BCA.
已知:如图,DA=CB,∠ADC=∠BCD.求证:∠ADB=∠BCA. 已知∠1=∠2,AC=BD,E,F,A,B在同一直线上,问∠3=∠4吗?
已知∠1=∠2,AC=BD,E,F,A,B在同一直线上,问∠3=∠4吗?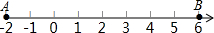 如图,数轴上A,B两点表示的数分别为-2和6,数轴上的点C是AB的中点,数轴上点D,使AD=$\frac{3}{2}$AC,则线段BD的长是2或14.
如图,数轴上A,B两点表示的数分别为-2和6,数轴上的点C是AB的中点,数轴上点D,使AD=$\frac{3}{2}$AC,则线段BD的长是2或14. 如图,点E,F在AC上,AB∥CD,AB=CD,AE=CF.求证:BF=DE.
如图,点E,F在AC上,AB∥CD,AB=CD,AE=CF.求证:BF=DE.