题目内容
19．
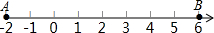如图，数轴上A，B两点表示的数分别为-2和6，数轴上的点C是AB的中点，数轴上点D，使AD=$\frac{3}{2}$AC，则线段BD的长是2或14．
分析 此题根据题意先求出AC和BC的长，然后再求出AD的长，要注意对点D的位置进行分类讨论．
解答 解：∵A，B两点表示的数分别为-2和6，
∴AB=6-（-2）=8，
∵AC=BC=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4，
∵AD=$\frac{3}{2}$AC=$\frac{3}{2}$×4=6，
当点D在点A右侧时，BD=AB-AD=8-6=2，
当点D在点A左侧时，BD=AB+BD=8+6=14，
故答案为2或14．
点评 本题考查了两点间的距离，数轴，主要利用了线段中点的定义，数轴上两点间距离的求法，要注意分类讨论．
练习册系列答案
阅读快车系列答案
相关题目
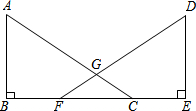已知，如图，点B、F、C、E在同一直线上，AC、DF相交于点G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AC=DF，BF=CE，求证：∠A=∠D．
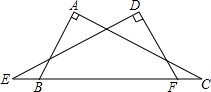如图所示，E、B、F、C在同一条直线上，若∠D=∠A=90°，EB=FC，AB=DF，∠ABC=70°，AC=4．求∠E的度数和DE的长．
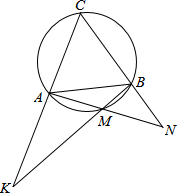如图，已知等边△ABC内接于圆，圆的半径为$\frac{\sqrt{3}}{2}$，在劣弧AB上取异于A、B的点M．如果设直线AC与BM相交于K，直线CB与AM相交于点N，则线段AK•BN的值为$\frac{9}{4}$．
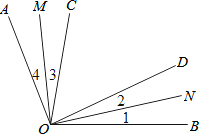如图，已知∠AOB=120°，∠COD=50°，OM平分∠BOD，即∠1=∠2，ON平分∠AOC，即∠3=∠4；