题目内容
20.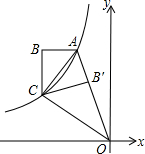 如图,双曲线y=-$\frac{3}{x}$(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则三角形OAC的面积是$\frac{9}{4}$.
如图,双曲线y=-$\frac{3}{x}$(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则三角形OAC的面积是$\frac{9}{4}$.
分析 设BC的延长线交x轴于点D,连接OC,点C(-m,n),AB=a,由角平分线的性质得,CD=CB′,则△OCD≌△OCB′,再由翻折的性质得,BC=B′C,根据反比例函数的性质,可得出S△OCD=$\frac{1}{2}$mn=$\frac{3}{2}$,由AB∥x轴,得点A(a-m,2n),由题意得2n(a-m)=-3,从而得出三角形ABC的面积等于$\frac{1}{2}$an,即可得出答案.
解答 解:设BC的延长线交x轴于点D,
设点C(-m,n),AB=a,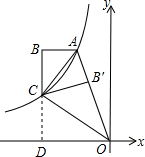
∵∠ABC=90°,AB∥x轴,
∴CD⊥x轴,
由折叠的性质可得:∠AB′C=∠ABC=90°,
∴CB′⊥OA,
∵OC平分OA与x轴负半轴的夹角,
∴CD=CB′,
在Rt△OB′C和Rt△ODC中,
∵$\left\{\begin{array}{l}{CB′=CD}\\{OC=OC}\end{array}\right.$,
∴Rt△OCD≌Rt△OCB′(HL),
再由翻折的性质得,BC=B′C,
∴BC=CD,
∴点B(-m,2n),
∵双曲线y=-$\frac{3}{x}$(x<0)经过四边形OABC的顶点A、C,
∴S△OCD=$\frac{1}{2}$|mn|=$\frac{3}{2}$,
∴S△OCB′=S△OCD=$\frac{3}{2}$,
∵AB∥x轴,
∴点A(a-m,2n),
∴2n(a-m)=-3,
∴an-mn=-$\frac{3}{2}$,
∵mn=3
∴an=$\frac{3}{2}$,
∴S△ABC=$\frac{1}{2}$an=$\frac{3}{4}$,
∴S△OAC=S△OCB′+S△ABC=$\frac{3}{2}$+$\frac{3}{4}$=$\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本题考查了翻折变换-折叠问题,全等三角形的判定和性质,三角形的面积的求法,熟练掌握折叠的性质是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案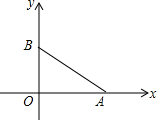 如图,线段AB的两个端点坐标分别为A($\sqrt{3}$,0)、B(0,1).
如图,线段AB的两个端点坐标分别为A($\sqrt{3}$,0)、B(0,1).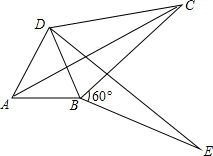 给出定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
给出定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.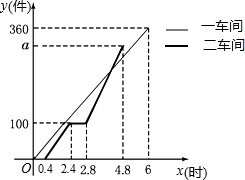 某工厂安排第一、二两个车间的工人加工某种商品,第一车间加工0.4小时后,第二车间开始工作,第二车间工作中有一次停产更换设备,更换设备后,第二车间的工作效率是原来的2倍,两车间各自加工商品的数量y(件)与时间x(时)的函数图象如图所示:
某工厂安排第一、二两个车间的工人加工某种商品,第一车间加工0.4小时后,第二车间开始工作,第二车间工作中有一次停产更换设备,更换设备后,第二车间的工作效率是原来的2倍,两车间各自加工商品的数量y(件)与时间x(时)的函数图象如图所示: 如图,矩形ABCD中,点E、F在边AD上,AF=DE,求证:BE=CF.
如图,矩形ABCD中,点E、F在边AD上,AF=DE,求证:BE=CF.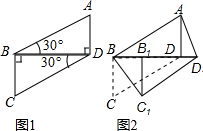 将两块全等的直角三角形如图1摆放在一起,设较短直角边为1.现将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置(如图2).
将两块全等的直角三角形如图1摆放在一起,设较短直角边为1.现将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置(如图2).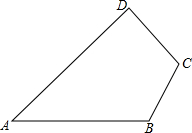 如图所示,在四边形ABCD中,BC=CD=10,∠B=∠C=120°,∠A=45°,求四边形ABCD的面积.
如图所示,在四边形ABCD中,BC=CD=10,∠B=∠C=120°,∠A=45°,求四边形ABCD的面积.