题目内容
9.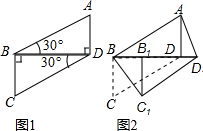 将两块全等的直角三角形如图1摆放在一起,设较短直角边为1.现将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置(如图2).
将两块全等的直角三角形如图1摆放在一起,设较短直角边为1.现将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置(如图2).(1)求证:四边形ABC1D1是平行四边形;
(2)当四边形ABC1D1为矩形时,求矩形ABC1D1的面积;
(3)当点B的移动距离为多少时,四边形ABC1D1为菱形.
分析 (1)欲证明四边形ABC1D1是平行四边形,只需推知:AB=C1D1,AB∥C1D1即可;
(2)只要∠BC1D1=90°,四边形ABC1D1即为矩形,所以求得Rt△BB1C1的面积即可易求矩形ABC1D1的面积;
(3)当点B的移动距离为$\sqrt{3}$时,D、B1两点重合,根据对角线互相垂直平分的四边形是菱形,可判定四边形ABC1D1为菱形.
解答 (1)证明:根据平移的性质得到:△ABD≌△CDB≌△C1D1B1,
∴AB=C1D1.
又∵∠ABD=∠C1D1B=30°,
∴AB∥C1D1,
∴四边形ABC1D1是平行四边形;
(2)解:∵在移动过程中,四边形ABC1D1恒为平行四边形,
∴只要∠BC1D1=90°,四边形ABC1D1即为矩形,
此时在Rt△BB1C1中,B1C1=1,∠BB1C1=90°,∠B1BC1=60°,
∴BC1=2BB1,由勾股定理得,BC1=$\frac{2\sqrt{3}}{3}$,
由已知得:AB=2,
∴S矩形ABC1D1=$\frac{2\sqrt{3}}{3}$×2=$\frac{4\sqrt{3}}{3}$;
(3)解:当四边形ABC1D是菱形时,∠ABD1=∠C1BD1=30°,
∵B1C1=1,
∴BB1=$\frac{{B}_{1}{C}_{1}}{tan30°}$=$\frac{1}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$,
当点B的移动距离为$\sqrt{3}$时,四边形ABC1D1为菱形.
点评 此题主要考查平行四边形、矩形、菱形的判定,综合利用了直角三角形的性质,注意:有一直角的平行四边形是矩形,菱形的每一条对角线平分一组对角.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
14.某书店要经营一种新上市的中考数学复习资料,进价为每本20元,试营销阶段发现每天的销售量y(本)与单价x(元/本)之间满足如表:
(1)观察并分析表中的y与x之间的对应关系,用学过的一次函数、反比例函数或二次函数的有关知识写出y(本)与x(元/本)的函数解析式.
(2)写出书店销售这种中考数学复习资料,每天所得的销售利润W(元)与销售单价x(元/本)之间的函数解析式,并求出销售单价为多少时,该书店每天的销售利润最大,最大利润是多少?
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过26元;
方案B:每天销售量不少于50本,且每本资料的利润至少为18元
请比较哪种方案的最大利润更高,并说明理由.
| 销售价格x(元/本) | … | 25 | 30 | 35 | 40 | … |
| 销售量y(本) | … | 250 | 200 | 150 | 100 | … |
(2)写出书店销售这种中考数学复习资料,每天所得的销售利润W(元)与销售单价x(元/本)之间的函数解析式,并求出销售单价为多少时,该书店每天的销售利润最大,最大利润是多少?
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过26元;
方案B:每天销售量不少于50本,且每本资料的利润至少为18元
请比较哪种方案的最大利润更高,并说明理由.
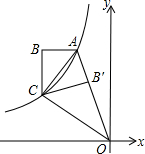 如图,双曲线y=-$\frac{3}{x}$(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则三角形OAC的面积是$\frac{9}{4}$.
如图,双曲线y=-$\frac{3}{x}$(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则三角形OAC的面积是$\frac{9}{4}$.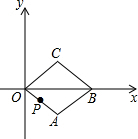 如图,在平面直角坐标系xOy中,菱形OABC的顶点B在x轴上,OA=1,∠AOC=60°.当菱形OABC开始以每秒转动60度的速度绕点O逆时针旋转时,动点P同时从点O出发,以每秒1个单位的速度沿菱形OABC的边逆时针运动.当运动时间为1秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);当运动时间为2015秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
如图,在平面直角坐标系xOy中,菱形OABC的顶点B在x轴上,OA=1,∠AOC=60°.当菱形OABC开始以每秒转动60度的速度绕点O逆时针旋转时,动点P同时从点O出发,以每秒1个单位的速度沿菱形OABC的边逆时针运动.当运动时间为1秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);当运动时间为2015秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$). 如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,∠B=54°,则∠BEF=126°.
如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,∠B=54°,则∠BEF=126°.