题目内容
10.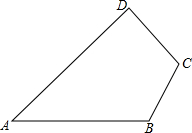 如图所示,在四边形ABCD中,BC=CD=10,∠B=∠C=120°,∠A=45°,求四边形ABCD的面积.
如图所示,在四边形ABCD中,BC=CD=10,∠B=∠C=120°,∠A=45°,求四边形ABCD的面积.
分析 根据BC=CD,∠C=120°,那么△BCD的面积所需要的值可利用勾股定理求解,所以应连接BD,构造等腰三角形,同时根据∠B=120°以及等腰三角形的底角可得到△ABD是一个直角三角形,那么把四边形进行分割计算即可.
解答 解:连接BD,过C作CE⊥BD于E,
∵BC=DC=10米,∠ABC=∠BCD=120°,
∴∠1=∠2=30°,
∴∠ABD=90°,
∴CE=5米,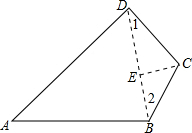
∴BE=$\sqrt{B{C}^{2}-C{E}^{2}}$=5$\sqrt{3}$,
∵∠A=45°,
∴AB=BD=2BE=10$\sqrt{3}$,
∴S四边形ABCD=S△ABD+S△BCD,
=$\frac{1}{2}$AB•BD+$\frac{1}{2}$BD•CE,
=$\frac{1}{2}$×10$\sqrt{3}$×10$\sqrt{3}$+$\frac{1}{2}$×10$\sqrt{3}$×5$\sqrt{3}$=150+25$\sqrt{3}$.
点评 本题考查了勾股定理的运用,等腰三角形的性质以及对多边形面积的求法,解题的关键是通过作辅助线可将问题进行转化,两个直角三角形面积相减可即所求四边形的面积.

练习册系列答案
相关题目
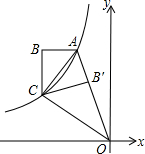 如图,双曲线y=-$\frac{3}{x}$(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则三角形OAC的面积是$\frac{9}{4}$.
如图,双曲线y=-$\frac{3}{x}$(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则三角形OAC的面积是$\frac{9}{4}$. 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为10和6时,则阴影部分的面积为15.
如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为10和6时,则阴影部分的面积为15.