题目内容
8.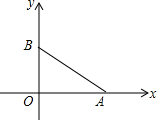 如图,线段AB的两个端点坐标分别为A($\sqrt{3}$,0)、B(0,1).
如图,线段AB的两个端点坐标分别为A($\sqrt{3}$,0)、B(0,1).(1)尺规作图:以AB为边在第一象限内作等边△ABC(保留作图痕迹,可不写做法);
(2)求过A、B两点直线的函数解析式;
(3)求△ABC的面积;
(4)如果第一象限内有一点P(m,$\frac{1}{2}$),且△ABP的面积与△ABC的面积相等,求m的值.
分析 (1)分别以点B,点A为圆心,以AB为半径画弧交于点C,△ABC就是所求的等边三角形,
(2)过A、B两点直线的函数解析式为y=kx+b,把点A($\sqrt{3}$,0)、B(0,1)代入求出k,b的值,即可得出过A、B两点直线的函数解析式,
(3)作CD⊥AB,由△ABC是等边三角形,可得CD=$\sqrt{3}$,由S△ABC=$\frac{1}{2}$AB•CD求解即可,
(4)过点C作AB的平行线,过BO的中点作x轴的平行线,两线交于点P,由同底等高的三角形面积可得S△ABP=S△ABC,作CD⊥y轴,BC=AB=2,∠OBA=60°,∠CBA=60°,可得∠CBD=60°,利用特殊直角三角形得CD=$\sqrt{3}$,BD=1,从而得出C的坐标,设直线CP的解析式为y=-$\frac{\sqrt{3}}{3}$x+b,把C($\sqrt{3}$,2)代入得b的值,从而得出直线CP的解析式,把y=$\frac{1}{2}$代入得x的值即可得出点P的坐标.
解答 解:(1)如图1,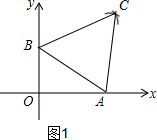
(2)设过A、B两点直线的函数解析式为y=kx+b,
把点A($\sqrt{3}$,0)、B(0,1)代入得$\left\{\begin{array}{l}{\sqrt{3}k+b=0}\\{b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=1}\end{array}\right.$,
∴过A、B两点直线的函数解析式为y=-$\frac{\sqrt{3}}{3}$x+1,
(3)∵A($\sqrt{3}$,0)、B(0,1).
∴OA=$\sqrt{3}$,OB=1,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2,
如图2,作CD⊥AB,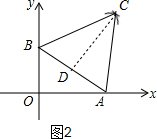
∵△ABC是等边三角形,
∴CD=$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
(3)如图3,过点C作AB的平行线,过BO的中点作x轴的平行线,两线交于点P,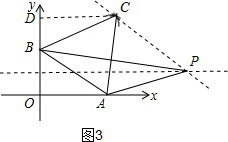
由同底等高的三角形面积可得S△ABP=S△ABC,
作CD⊥y轴,
∵BC=AB=2,∠OBA=60°,∠CBA=60°,
∴∠CBD=60°,
∴CD=$\sqrt{3}$,BD=1,
∴C($\sqrt{3}$,2),
设直线CP的解析式为y=-$\frac{\sqrt{3}}{3}$x+b,
把C($\sqrt{3}$,2)代入得,2=-1+b,解得b=3,
∴直线CP的解析式为y=-$\frac{\sqrt{3}}{3}$x+3,
把y=$\frac{1}{2}$代入得$\frac{1}{2}$=-$\frac{\sqrt{3}}{3}$x+3,解得x=$\frac{5\sqrt{3}}{2}$,
∴P($\frac{5\sqrt{3}}{2}$,$\frac{1}{2}$).
点评 本题主要考查了一次函数综合题,涉及用待定系数法求解析式,等边三角形的性质,勾股定理等知识,解题的关键是正确的作出辅助线求解.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案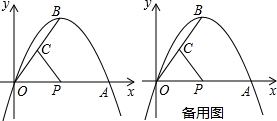
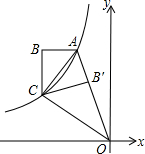 如图,双曲线y=-$\frac{3}{x}$(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则三角形OAC的面积是$\frac{9}{4}$.
如图,双曲线y=-$\frac{3}{x}$(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则三角形OAC的面积是$\frac{9}{4}$.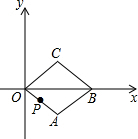 如图,在平面直角坐标系xOy中,菱形OABC的顶点B在x轴上,OA=1,∠AOC=60°.当菱形OABC开始以每秒转动60度的速度绕点O逆时针旋转时,动点P同时从点O出发,以每秒1个单位的速度沿菱形OABC的边逆时针运动.当运动时间为1秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);当运动时间为2015秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
如图,在平面直角坐标系xOy中,菱形OABC的顶点B在x轴上,OA=1,∠AOC=60°.当菱形OABC开始以每秒转动60度的速度绕点O逆时针旋转时,动点P同时从点O出发,以每秒1个单位的速度沿菱形OABC的边逆时针运动.当运动时间为1秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);当运动时间为2015秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).