题目内容
16.(1)计算:(3-π)0+(-$\frac{1}{3}$)-2+$\sqrt{8}$-2|sin45°-1|;(2)先化简,再求值:$(1+\frac{1}{{{m^2}-1}})÷(m-\frac{m}{m+1})$,其中实数m使关于x的一元二次方程x2-4x-m=0有两个相等的实数根.
分析 (1)利用零指数幂、负整数指数幂和特殊角的三角函数值进行计算;
(2)先把括号内通分后进行同分母的减法运算,再把除法运算化为乘法运算,接着约分得到原式=$\frac{1}{m-1}$,然后根据判别式的意义求出m的值,再把m的值代入原式=$\frac{1}{m-1}$中计算即可.
解答 解:(1)原式=1+9+2$\sqrt{2}$-2|$\frac{\sqrt{2}}{2}$-1)
=10+2$\sqrt{2}$+2($\frac{\sqrt{2}}{2}$-1)
=10+2$\sqrt{2}$+$\sqrt{2}$-2
=8+3$\sqrt{2}$;
(2)原式=$\frac{{m}^{2}+1-1}{(m+1)(m-1)}$÷$\frac{m(m+1)-m}{m+1}$
=$\frac{{m}^{2}}{(m+1)(m-1)}$•$\frac{m+1}{{m}^{2}}$
=$\frac{1}{m-1}$,
∵一元二次方程x2-4x-m=0有两个相等的实数根,
∴△=(-4)2-4(-m)=0,
∴m=-4,
当m=-4时,原式=$\frac{1}{-4-1}$=$-\frac{1}{5}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了实数的运算和根的判别式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.服装店销售某款服装,每件服装的标价为300元,若按标价的八折销售,仍可获利60元,则这款服装每件的标价比进价多( )
| A. | 60元 | B. | 80元 | C. | 120元 | D. | 180元 |
5.下列式子不正确的是( )
| A. | ${2^{-1}}=\frac{1}{2}$ | B. | (-2)-2=4 | C. | ${({\frac{1}{2}})^{-3}}$=8 | D. | (-2)0=1 |
 如图,△ABC中,AB=AC,∠C=70°,作AB的垂直平分线交AB于E,交AC于D,求∠DBC的度数.
如图,△ABC中,AB=AC,∠C=70°,作AB的垂直平分线交AB于E,交AC于D,求∠DBC的度数.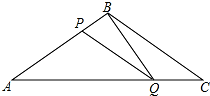 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.