题目内容
2.已知△ABC是等边三角形,点D是直线AC上的点,点E是直线BC上的点,且DB=DE,(1)当点D在线段AC上(不与A,C重合)时,易证AD=CE;
(2)当点D在CA的延长线上;如图(3),当点D在AC的延长线上时,线段AD与CE有怎样的数量关系,直接写出你的猜想,并在图(2)和图(3)中选择一种情况给予证明.
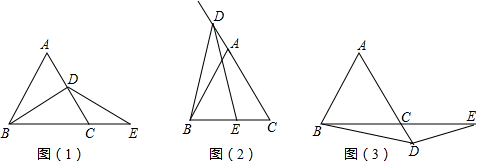
分析 (1)如图1中,作DM∥AB交CB于M.首先证明AD=BM.再证明△DBM≌△DEC,推出BM=CE,即可证明;
(2)如图2中,作DM∥AB交CB的延长线于M.首先证明AD=BM.再证明△DBM≌△DEC,推出BM=CE,即可证明;如图3中,作DM∥AB交BC的延长线于M.证明方法类似;
解答 解:(1)如图1中,作DM∥AB交CB于M.
∵△ABC是等边三角形,
∴∠ABC=∠DMC=60°,∠BAC=∠MDC=60°,
∴△DMC是等边三角形,
∴DM=DC=CM,∠DMC=∠DCM=60°,
∴∠DMB=∠DCE
∵CA=CB,
∴BM=AD,
∵DB=DE,
∴∠DBE=∠E,
在△DBM和△DEC中,
$\left\{\begin{array}{l}{∠DBM=∠E}\\{∠DMB=∠DCE}\\{DB=DE}\end{array}\right.$,
∴△DBM≌△DEC,
∴BM=CE,
∴AD=EC.
(2)结论:不变.AD=EC.
理由:如图2中,作DM∥AB交CB的延长线于M.
∵△ABC是等边三角形,
∴∠ABC=∠M=60°,∠BAC=∠MDC=60°,
∴△DMC是等边三角形,
∴DM=DC=CM,∠M=∠C=60°,
∵CA=CB,
∴BM=AD,
∵DB=DE,
∴∠DBE=∠DEB,
∴∠DBM=∠DEC,
在△DBM和△DEC中,
$\left\{\begin{array}{l}{∠M=∠C}\\{∠DBM=∠DEC}\\{DB=DE}\end{array}\right.$,
∴△DBM≌△DEC,
∴BM=CE,
∴AD=EC.
如图3中,作DM∥AB交BC的延长线于M.
∵△ABC是等边三角形,
∴∠ABC=∠DMC=60°,∠BAC=∠MDC=60°,
∴△DMC是等边三角形,
∴DM=DC=CM,∠DMB=∠DCM=60°,
∵CA=CB,
∴BM=AD,
∵DB=DE,
∴∠DBE=∠DEB,
∴∠DBM=∠DEC,
在△DBM和△DEC中,
$\left\{\begin{array}{l}{∠DMB=∠DCE}\\{∠DBM=∠E}\\{DM=DC}\end{array}\right.$,
∴△DBE≌△DEC,
∴BM=CE,
∴AD=EC.
点评 本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.


 如图,BD=CD,DE⊥AB,DF⊥AC,DE=DF,∠A=90°,试说明:AB=AC.
如图,BD=CD,DE⊥AB,DF⊥AC,DE=DF,∠A=90°,试说明:AB=AC. 如图,已知在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于点E,EF⊥AB于点F.求证:AC=AF.
如图,已知在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于点E,EF⊥AB于点F.求证:AC=AF.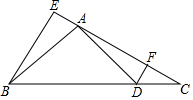 如图,在△ABC中,AB=AC,过A作AD⊥AB交BC于点D,过B作BE⊥AC,交CA延长线于点E,过D作DF⊥AC,垂足为F.若EF=3$\sqrt{3}$.BC=6$\sqrt{2}$.则tan∠C=$\frac{\sqrt{2}}{2}$.
如图,在△ABC中,AB=AC,过A作AD⊥AB交BC于点D,过B作BE⊥AC,交CA延长线于点E,过D作DF⊥AC,垂足为F.若EF=3$\sqrt{3}$.BC=6$\sqrt{2}$.则tan∠C=$\frac{\sqrt{2}}{2}$. 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,BE=CF,求证:AC∥DF.
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,BE=CF,求证:AC∥DF.