题目内容
18.已知二次函数y=ax2+bx+c(a≠0)与x轴的交点坐标为A(m,0),B(n,0),点A在点B的左边,当ax2+bx+c=2015时有实数根x1,x2(x1<x2),以下说法中不正确的是( )| A. | 当a>0时,x1<m<n<x2 | |
| B. | 当a<0时,m<x1<x2<n | |
| C. | 存在m+n=x1+x2 | |
| D. | y=ax2+bx+c-2015与x轴的交点坐标不可能是(x1,0),(x2,0) |
分析 令y=ax2+bx+c-2015,则该函数图象相当于y=ax2+bx+c向下平移2015个单位得到的,结合图象可判断选项,可得出答案.
解答 解:
方程ax2+bx+c=2015可化为ax2+bx+c-2015=0,
令y=ax2+bx+c-2015,则该函数图象相当于y=ax2+bx+c向下平移2015个单位得到,
当a>时,如图1,则有x1<m<n<x2,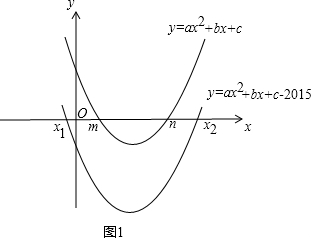
故A正确;
当a<0时,如图2,则有m<x1<x2<n,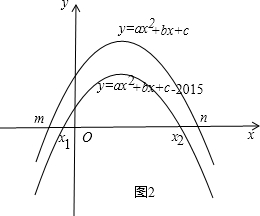
故B正确;
由两函数图象有共同的对称轴,
∴$\frac{m+n}{2}$=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{b}{2a}$,
故C正确;
∵方程ax2+bx+c=2015的两根分别为x1和x2,
∴y=ax2+bx+c-2015与x轴的交点坐标为(x1,0),(x2,0),
故D不正确;
故选D.
点评 本题主要考查二次函数与一元二次方程的关系,掌握二次函数图象的交点横坐标为对应一元二次方程的两根是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,⊙O是△ABC的外接圆,连接OA,OB,∠OBA=48°,则∠C的度数为42°.
如图,⊙O是△ABC的外接圆,连接OA,OB,∠OBA=48°,则∠C的度数为42°.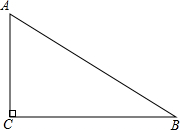 除了大家熟知的创建全国文明城市外,淮北目前也正在创建全国绿化模范城市,其中把原有的绿地扩充改造就是创建工程计划之一.如图,现有一块直角三角形的绿地,量得两直角边分别为9米和12米,需要将绿地扩大改造为等腰三角形,且扩充的部分是以BC边为直角边的直角三角形,求扩充后等腰三角形的周长.
除了大家熟知的创建全国文明城市外,淮北目前也正在创建全国绿化模范城市,其中把原有的绿地扩充改造就是创建工程计划之一.如图,现有一块直角三角形的绿地,量得两直角边分别为9米和12米,需要将绿地扩大改造为等腰三角形,且扩充的部分是以BC边为直角边的直角三角形,求扩充后等腰三角形的周长.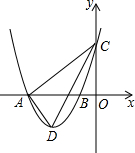 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(-4,0)、B(-l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(-4,0)、B(-l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点. 平行四边形ABCD中,EF平行于对角线AC,且与AB,BC分别交于E,F,求证:S△ADE=S△CDF.
平行四边形ABCD中,EF平行于对角线AC,且与AB,BC分别交于E,F,求证:S△ADE=S△CDF. 小朋从镜子中看到汽车车牌的部分号码如图所示,则该车牌照的部分号码为E6395.
小朋从镜子中看到汽车车牌的部分号码如图所示,则该车牌照的部分号码为E6395.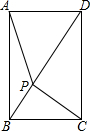 如图,点P是矩形ABCD对角线BD上的一个动点,已知AB=2,BC=$\sqrt{3}$,则PA+PB+PC的最小值是$\sqrt{13}$.
如图,点P是矩形ABCD对角线BD上的一个动点,已知AB=2,BC=$\sqrt{3}$,则PA+PB+PC的最小值是$\sqrt{13}$.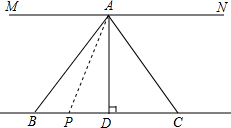 已知:如图,AD平分∠BAC,且AD⊥BC于点D,MN∥BC,请在括号中补全步骤的推理理由.
已知:如图,AD平分∠BAC,且AD⊥BC于点D,MN∥BC,请在括号中补全步骤的推理理由.