题目内容
14.直角坐标系中,点A坐标为(5,-3),B坐标为(1,0),将点A绕点B逆时针旋转90°得到点C,则点C的坐标为(4,4).分析 根据题意画出图形,易证△ADB≌△BEC,求出CE、OE的长即可求出C的坐标.
解答  解:如图所示,点A绕点B逆时针旋转90°到点C,
解:如图所示,点A绕点B逆时针旋转90°到点C,
∵A坐标为(5,-3),B坐标为(1,0),
∴AD=3,BD=4,
∴AB=5,
根据旋转的性质,AB=BC,
∵∠ABC=90°
∴∠EBC+∠ABD=90°,
∵∠DAB+∠ABD=90°,
∴∠EBC=∠DAB.
在△EBC和△BAD中
$\left\{\begin{array}{l}{∠CEB=∠BDA=90°}\\{∠EBC=∠DAB}\\{AB=BC}\end{array}\right.$,
∴△EBC≌△BAD,
∴CE=BD=4,BE=AD=3,
∵OB=1,
∴OE=4,
∴C(4,4).
故答案为:(4,4).
点评 本题主要考查了旋转变换和三角形全等的判定与性质,证明△EBC≌△BAD是解决问题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
5.某商店有两个进价不同的计算器都以64元卖出,其中一个盈利60%,另一个亏本20%,则该商店在这次买卖中( )
| A. | 不赔不赚 | B. | 赚了8元 | C. | 赔8元 | D. | 赚32元 |




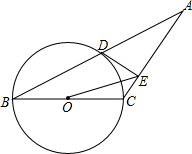 如图,在△ABC中,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
如图,在△ABC中,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
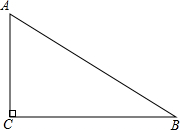 除了大家熟知的创建全国文明城市外,淮北目前也正在创建全国绿化模范城市,其中把原有的绿地扩充改造就是创建工程计划之一.如图,现有一块直角三角形的绿地,量得两直角边分别为9米和12米,需要将绿地扩大改造为等腰三角形,且扩充的部分是以BC边为直角边的直角三角形,求扩充后等腰三角形的周长.
除了大家熟知的创建全国文明城市外,淮北目前也正在创建全国绿化模范城市,其中把原有的绿地扩充改造就是创建工程计划之一.如图,现有一块直角三角形的绿地,量得两直角边分别为9米和12米,需要将绿地扩大改造为等腰三角形,且扩充的部分是以BC边为直角边的直角三角形,求扩充后等腰三角形的周长. 平行四边形ABCD中,EF平行于对角线AC,且与AB,BC分别交于E,F,求证:S△ADE=S△CDF.
平行四边形ABCD中,EF平行于对角线AC,且与AB,BC分别交于E,F,求证:S△ADE=S△CDF.