题目内容
3．计算：①解方程$\frac{x+1}{x-1}$-$\frac{4}{{x}^{2}-1}$=1；
②（$\frac{1}{2}$）-1-（3.14-π）0+0.254×44．
分析 ①分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解；
②原式利用零指数幂、负整数指数幂法则计算即可得到结果．
解答 解：①去分母得：x2+2x+1-4=x2-1，
解得：x=1，
经检验x=1是增根，分式方程无解；
②原式=2-1+1=2．
点评 此题考查了解分式方程，以及实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
如图，将一副三角尺的直角顶点O重合，摆放在桌面上，若∠AOD=156°，则∠BOC=24°．
15．
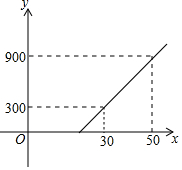某旅客携带x（公斤）的行李乘飞机，登机前，旅客可选择托运或快递行李，托运费y1（元）与行李质量x（公斤）的对应关系由如图所示的一次函数图象确定，下表列出了快递费y2（元）与行李质量x（公斤）的对应关系，
（1）如果旅客选择托运，求可携带的免费行李的最大质量为多少公斤？
（2）如果旅客选择快递，当1≤x≤15时，求快递费y2（元）与行李质量x（公斤）的函数关系式；
（3）某旅客携带25公斤的行李，设托运m（公斤）行李（10≤m＜24，m为正整数），剩下的行李选择快递，m为何值时，总费用y的值最小，总费用的最小值是多少？
某旅客携带x（公斤）的行李乘飞机，登机前，旅客可选择托运或快递行李，托运费y1（元）与行李质量x（公斤）的对应关系由如图所示的一次函数图象确定，下表列出了快递费y2（元）与行李质量x（公斤）的对应关系，| 行李的质量x（公斤） | 快递费 |
| 不超过1公斤 | 10元 |
| 超过1公斤但不超过5公斤的部分 | 3元/公斤 |
| 超过5公斤但不超过15公斤的部分 | 5元/公斤 |
（2）如果旅客选择快递，当1≤x≤15时，求快递费y2（元）与行李质量x（公斤）的函数关系式；
（3）某旅客携带25公斤的行李，设托运m（公斤）行李（10≤m＜24，m为正整数），剩下的行李选择快递，m为何值时，总费用y的值最小，总费用的最小值是多少？
如图所示，把长方形ABCD沿EF折叠，若∠1=48°，则∠AEF等于114°．