题目内容
10.实数$\sqrt{{π}^{2}}$,$\sqrt{0.09},\frac{12}{7},0,\sqrt{\frac{1}{36}},0.1010010001…,\sqrt{0.4}$,-$\root{3}{100}$中,无理数的个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据无理数的三种形式求解.
解答 解:$\sqrt{{π}^{2}}$=π,$\sqrt{0.09}$=0.3,$\sqrt{\frac{1}{36}}$=$\frac{1}{6}$,$\sqrt{0.4}$=$\frac{\sqrt{10}}{5}$,
所给数据中无理数有:$\sqrt{{π}^{2}}$,0.1010010001…,$\sqrt{0.4}$,-$\root{3}{100}$,共4个.
故选C.
点评 本题考查了无理数的知识,解答本题的关键是掌握无理数的三种形式,①开方开不尽的数,②无限不循环小数,③含有π的数.

练习册系列答案
相关题目
18.在平面直角坐标系中,已知直线$y=-\frac{3}{4}x+3$与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则n的值是( )
| A. | 3或4 | B. | 3或12 | C. | 3或-4 | D. | $\frac{4}{3}$或-12 |
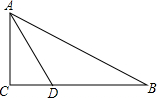 如图,△ABC的三边分别为AC=5,BC=12,AB=13,将△ABC沿AD折叠,使AC落在AB上.
如图,△ABC的三边分别为AC=5,BC=12,AB=13,将△ABC沿AD折叠,使AC落在AB上. 如图,将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处,AB=6,BC=10
如图,将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处,AB=6,BC=10