题目内容
5. 如图,将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处,AB=6,BC=10
如图,将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处,AB=6,BC=10(1)求证:△AEF∽△DFC;
(2)求线段EF的长度.
分析 (1)由四边形ABCD是矩形,于是得到∠A=∠D=∠B=90°,根据折叠的性质得∠EFC=∠B=90°,推出∠AEF=∠DFC,即可得到结论;
(2)根据折叠的性质得CF=BC=10,根据勾股定理得到DF=$\sqrt{C{F}^{2}-C{D}^{2}}$=8,求得AF=2,然后根据勾股定理列方程即可得到结论.
解答 解:(1)∵四边形ABCD是矩形,
∴∠A=∠D=∠B=90°,
根据折叠的性质得∠EFC=∠B=90°,
∴∠AFE+∠AEF=∠AFE+∠DFC=90°,
∴∠AEF=∠DFC,
∴△AEF∽△DFC;
(2)根据折叠的性质得:CF=BC=10,
∴DF=$\sqrt{C{F}^{2}-C{D}^{2}}$=8,
∴AF=2,
∵AE=AB-BE=6-EF,
∴EF2=AE2+AF2,
即EF2=(6-EF)2+22,
解得:EF=$\frac{10}{3}$.
点评 该题主要考查了相似三角形的判定和性质,矩形的性质、翻折变换的性质及其应用问题;解题的关键是灵活运用矩形的性质、翻折变换的性质来分析、判断、解答.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
10.实数$\sqrt{{π}^{2}}$,$\sqrt{0.09},\frac{12}{7},0,\sqrt{\frac{1}{36}},0.1010010001…,\sqrt{0.4}$,-$\root{3}{100}$中,无理数的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.下列整数中,小于-2的整数是( )
| A. | -3 | B. | -1 | C. | 2 | D. | 3 |
15.下列函数①y=2x;②y=$\frac{1}{2x}$;③y=2x+1;④y=2x2+1中,是一次函数的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
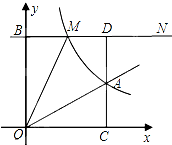 已知,如图,正比例函数y=ax的图象与反比例函数图象交于A点(3,2),
已知,如图,正比例函数y=ax的图象与反比例函数图象交于A点(3,2),