题目内容
16．在△ABC中，∠A，∠B都是锐角，且（sinA-$\frac{\sqrt{3}}{2}$）2+（tanB-1）2=0，则∠C=75°．分析 根据偶次幂具有非负性可得sinA-$\frac{\sqrt{3}}{2}$=0，tanB-1=0，再根据特殊角的三角函数值可得：∠A=60°，∠B=45°，然后再利用三角形内角和定理可得答案．
解答 解：由题意得：sinA-$\frac{\sqrt{3}}{2}$=0，tanB-1=0，
解得：∠A=60°，∠B=45°，
则∠C=180°-60°-45°=75°，
故答案为：75°．
点评 此题主要考查了特殊角的三角函数值，关键是掌握30°、45°、60°角的各种三角函数值．
练习册系列答案
相关题目
6．已知a＜0、b＞0且|a|＞|b|，则a、b、-a、-b的大小关系是（ ）
| A． | b＞-a＞a＞-b | B． | -b＞a＞-a＞b | C． | a＞-b＞-a＞b | D． | -a＞b＞-b＞a |
11．
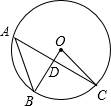如图，已知A，B，C三点在⊙O上，AC⊥BO于O，∠B=55°，则∠BOC的度数为（ ）
如图，已知A，B，C三点在⊙O上，AC⊥BO于O，∠B=55°，则∠BOC的度数为（ ）| A． | 45° | B． | 35° | C． | 70° | D． | 80° |
如图，已知CD是△ABC的高，且AC=8，BC=4$\sqrt{2}$，∠B=45°，求∠α的值．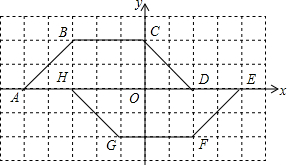
如图，网格平面直角坐标系中，组成网格的每个小正方形的边长为单位1．