题目内容
1. 如图,已知CD是△ABC的高,且AC=8,BC=4$\sqrt{2}$,∠B=45°,求∠α的值.
如图,已知CD是△ABC的高,且AC=8,BC=4$\sqrt{2}$,∠B=45°,求∠α的值.
分析 由CD是△ABC的高,于是得到∠BDC=∠ADC=90°,根据已知条件得到CD=BC•$\frac{\sqrt{2}}{2}$=4,然后求得cos∠α=$\frac{CD}{AC}=\frac{4}{8}$=$\frac{1}{2}$,即可得到结论.
解答 解:∵CD是△ABC的高,
∴∠BDC=∠ADC=90°,
∵∠B=45°,BC=4$\sqrt{2}$,
∴CD=BC•$\frac{\sqrt{2}}{2}$=4,
∵AC=8,
∴cos∠α=$\frac{CD}{AC}=\frac{4}{8}$=$\frac{1}{2}$,
∴∠α=60°.
点评 本题考查了解直角三角形,熟练掌握直角三角形的边角关系是解题的关键.

练习册系列答案
相关题目
9.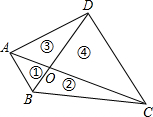 如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
 如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )| A. | ①②相似 | B. | ①③相似 | C. | ①④相似 | D. | ②相似 |
 已知:如图,在?ABCD中,E为AB的中点,EF∥BC,交CD于F.
已知:如图,在?ABCD中,E为AB的中点,EF∥BC,交CD于F.