题目内容
4．下列命题：①长度相等的弧是等弧；②任意三点确定一个圆；③相等的圆心角所对的弦相等；④外心在三角形的一条边上的三角形是直角三角形，其中真命题共有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 0个 |
分析 根据等弧的定义对①进行判断；根据确定圆的条件对②进行判断；根据圆心角、弧、弦的关系对③进行判断；根据圆周角定理的推论对④进行判断．
解答 解：完全重合的弧为等弧，长度相等的弧不一定是等弧，所以①错误；
任意不共线的三点确定一个圆，所以②错误；
在同圆或等圆轴，相等的圆心角所对的弦相等，所以③错误；
外心在三角形的一条边上的三角形是直角三角形，所以④正确．
故选A．
点评 本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．
练习册系列答案
名校课堂系列答案
相关题目
如图，将一块正方形的纸片沿虚线折叠两次，然后沿虚线剪掉一角，最后将剩余部分展开，得到的图案是（ ）
15．“十一”国庆期间，俄罗斯特技飞行队在黄山湖公园特技表演，其中一架飞机起飞后的高度变化如表：
（1）此时这架飞机比起飞点高了多少千米？
（2）如果飞机每上升或下降1千米需消耗2升燃油，那么这架飞机在这4个动作表演过程中，一共消耗了多少升燃油？
| 高度变化 | 记作 |
| 上升4.4km | 4.4km |
| 下降3.2km | -3.2km |
| 上升1.1km | +1.1km |
| 下降1.5km | -1.5km |
（2）如果飞机每上升或下降1千米需消耗2升燃油，那么这架飞机在这4个动作表演过程中，一共消耗了多少升燃油？
19．某汽车行驶时油箱中余油量Q（千克）与行驶时间t（小时）的关系如下：
（1）写出用时间t表示余油量Q的代数式：Q=40-4t；
（2）当t=$\frac{7}{4}$时，余油量Q的值是33；
（3）根据所列代数式回答，汽车行驶之前油箱中有油多少千克？
（4）邮箱中原有的汽油可供汽车行驶多少小时？
| 行驶时间t/h | 1 | 2 | 3 | 4 | 5 |
| 余油量Q/kg | 40-4 | 40-8 | 40-12 | 40-16 | 40-20 |
（2）当t=$\frac{7}{4}$时，余油量Q的值是33；
（3）根据所列代数式回答，汽车行驶之前油箱中有油多少千克？
（4）邮箱中原有的汽油可供汽车行驶多少小时？
9．
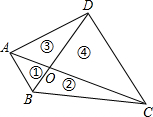如图，四边形ABCD的对角线AC、BD相交于O，且将这个四边形分成①②③④四个三角形．若OA：OC=OB：OD，则下列结论中一定正确的是（ ）
如图，四边形ABCD的对角线AC、BD相交于O，且将这个四边形分成①②③④四个三角形．若OA：OC=OB：OD，则下列结论中一定正确的是（ ）| A． | ①②相似 | B． | ①③相似 | C． | ①④相似 | D． | ②相似 |
