题目内容
11.解下列不等式组,并把解集在数轴上表示出来.(1)$\left\{\begin{array}{l}{\frac{x+1}{5}>\frac{3-x}{5},①}\\{4(x+4)<3(x+6);②}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3(x+1)>5x+4,①}\\{\frac{x-1}{2}≤\frac{2x-1}{3}.②}\end{array}\right.$.
分析 (1)先求出不等式组中每一个不等式的解集,再根据解集的规律:同大取大、同小取小、大小小大中间找、大大小小找不到,求出它们的公共部分,然后把不等式的解集表示在数轴上即可.
(2)先求出不等式组中每一个不等式的解集,再根据解集的规律:同大取大、同小取小、大小小大中间找、大大小小找不到,求出它们的公共部分,然后把不等式的解集表示在数轴上即可.
解答 解:(1)解不等式①得:x>1,
解不等式②得:x<2,
∴不等式组的解集为:1<x<2,
将不等式解集在数轴上表示如图: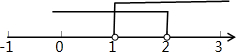
(2)解不等式①得:x<-$\frac{1}{2}$,
解不等式②得:x≥-1,
∴不等式组的解集为:-1≤x<-$\frac{1}{2}$,
将不等式解集表示在数轴上如图: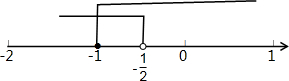
点评 此题主要考查了不等式组的解法,求不等式组的解集,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了,利用此规律得出不等式的解集是解题关键.

练习册系列答案
相关题目
19.直线y=kx+b与y=mx+n交于点(2,-1).则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ |
6.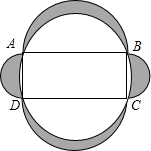 如图,已知矩形ABCD,且AB=12,AD=5.分别以AB、BC、CD、AD为直径画半圆;再以矩形ABCD的对角线AC为直径画圆,此圆通过A、B、C,D四点,则斜线部分面积为( )
如图,已知矩形ABCD,且AB=12,AD=5.分别以AB、BC、CD、AD为直径画半圆;再以矩形ABCD的对角线AC为直径画圆,此圆通过A、B、C,D四点,则斜线部分面积为( )
 如图,已知矩形ABCD,且AB=12,AD=5.分别以AB、BC、CD、AD为直径画半圆;再以矩形ABCD的对角线AC为直径画圆,此圆通过A、B、C,D四点,则斜线部分面积为( )
如图,已知矩形ABCD,且AB=12,AD=5.分别以AB、BC、CD、AD为直径画半圆;再以矩形ABCD的对角线AC为直径画圆,此圆通过A、B、C,D四点,则斜线部分面积为( )| A. | 60 | B. | 30 | C. | 60π | D. | 30π |
18. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠B=65°,则∠1的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠B=65°,则∠1的度数是( )
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠B=65°,则∠1的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠B=65°,则∠1的度数是( )| A. | 45° | B. | 25° | C. | 20° | D. | 15° |
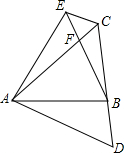 已知△ABC,将边AC绕点A顺时旋转60°得到AD,将AB绕点A逆时针旋转60°得到AE连接CD,CE,且点B在CD上
已知△ABC,将边AC绕点A顺时旋转60°得到AD,将AB绕点A逆时针旋转60°得到AE连接CD,CE,且点B在CD上
 一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A,B两点,且交y轴于点C.已知点A(1,4),点B在第三象限,且点B的横坐标为t(t<-1).
一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A,B两点,且交y轴于点C.已知点A(1,4),点B在第三象限,且点B的横坐标为t(t<-1).