题目内容
17. 一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A,B两点,且交y轴于点C.已知点A(1,4),点B在第三象限,且点B的横坐标为t(t<-1).
一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A,B两点,且交y轴于点C.已知点A(1,4),点B在第三象限,且点B的横坐标为t(t<-1).(1)求反比例函数的解析式;
(2)用含t的式子表示k,b;
(3)若△AOB的面积为3,求点B的坐标.
分析 (1)把点A(1,4)代入y=$\frac{m}{x}$即可得到结论;
(2)由点B的横坐标为t,得到B(t,$\frac{4}{t}$),把A,B的坐标代入y=kx+b,解方程组即可得到结果;
(3)根据三角形的面积列方程即可得到结论.
解答 解:(1)把点A(1,4)代入y=$\frac{m}{x}$得:m=4,
∴反比例函数的解析式为y=$\frac{4}{x}$;
(2)∵点B的横坐标为t,
∴B(t,$\frac{4}{t}$),
∴$\left\{\begin{array}{l}{4=k+b}\\{\frac{4}{t}=kt+b}\end{array}\right.$, ∴$\left\{\begin{array}{l}{k=-\frac{4}{t}}\\{b=\frac{4t+4}{t}}\end{array}\right.$;
∴$\left\{\begin{array}{l}{k=-\frac{4}{t}}\\{b=\frac{4t+4}{t}}\end{array}\right.$;
(3)∵OC=$\frac{4t+4}{t}$,
∴S△AOB=S△ACO+S△BCO=$\frac{1}{2}$•$\frac{4t+4}{t}$×(-t+1)=3,
∴t=-2,
∴点B的坐标(-2,-2).
点评 本题考查了反比例函数与一次函数的交点,待定系数法求函数的解析式,三角形的面积的计算,正确的理解题意是解题的关键.

练习册系列答案
相关题目
9.下列给出的式子一定是二次根式的是( )
| A. | $\sqrt{{a}^{2}-2}$ | B. | $\sqrt{{x}^{2}+2}$ | C. | $\sqrt{3-π}$ | D. | $\root{3}{a}$ |
6.下列式子中,正确的是( )
| A. | $\root{3}{-8}=-\root{3}{8}$ | B. | $-\sqrt{3.6}=-0.6$ | C. | $\sqrt{{{(-3)}^2}}=-3$ | D. | $\sqrt{36}=±6$ |
7.不等式组$\left\{\begin{array}{l}{x+9<5x+1}\\{x≥2x-3}\end{array}\right.$的解集是( )
| A. | x>2 | B. | x≤3 | C. | 2<x≤3 | D. | x≥3 |
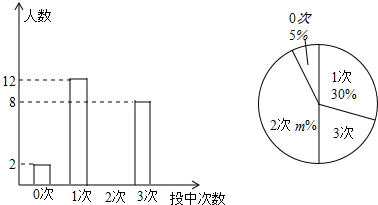
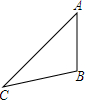 如图,△ABC中,∠B=100°,按要求完成画图并解答问题:
如图,△ABC中,∠B=100°,按要求完成画图并解答问题: 已知线段a和b,求作线段AB,使AB=2a-b.(不写作法,保留作图痕迹)
已知线段a和b,求作线段AB,使AB=2a-b.(不写作法,保留作图痕迹)