题目内容
8.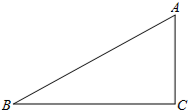 如图,在Rt△ABC中,∠C=90°,AC=3,tanB=$\frac{1}{2}$.
如图,在Rt△ABC中,∠C=90°,AC=3,tanB=$\frac{1}{2}$.(1)求BC的长;(2)求cosA的值.
分析 (1)运用三角函数的定义就可求出BC长;
(2)根据勾股定理可求出AB,然后运用三角函数的定义即可得到结论.
解答 解:(1)∵∠C=90°,AC=3,tanB=$\frac{1}{2}$,
∴tanB=$\frac{AC}{BC}$=$\frac{3}{BC}$=$\frac{1}{2}$,
∴BC=6;
(2)∵AC=3,BC=6,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=3$\sqrt{5}$,
∴cosA=$\frac{AC}{AB}$=$\frac{3}{3\sqrt{5}}$=$\frac{\sqrt{5}}{5}$.
点评 本题主要考查了三角函数的定义、勾股定理等知识,在直角三角形中,除直角外,只需知道两个元素(至少有一条边),就可求出另外的三个元素.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
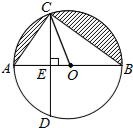 如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2.
如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2.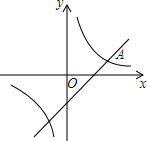 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=kx-2交于点A(3,1).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=kx-2交于点A(3,1).