题目内容
18.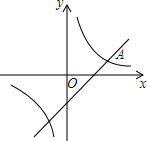 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=kx-2交于点A(3,1).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=kx-2交于点A(3,1).(1)求直线和双曲线的解析式;
(2)直线y=kx-2与x轴交于点B,点P是双曲线y=$\frac{m}{x}$上一点,过点P作直线PC∥x轴,交y轴于点C,交直线y=kx-2于点D.若DC=2OB,直接写出点P的坐标为P($\frac{3}{2}$,2)或(-$\frac{1}{2}$,-6).
分析 (1)把A的坐标分别代入双曲线y=$\frac{m}{x}$与直线y=kx-2,根据待定系数法即可求得;
(2)根据平行线分线段成比例定理得出$\frac{OF}{CF}$=$\frac{OB}{CD}$=$\frac{1}{2}$,得出CF=2OF,即可求得直线CD与y轴的交点坐标,从而求得P的纵坐标,代入(1)求得的解析式即可求得P点的坐标.
解答 解:(1)∵直线y=kx-2过点A(3,1),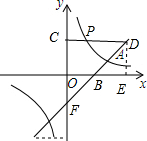
∴1=3k-2.
∴k=1.
∴直线的解析式为y=x-2.
∵双曲线y=$\frac{m}{x}$过点A(3,1),
∴m=3.
∴双曲线的解析式为$y=\frac{3}{x}$.
(2)$({\frac{3}{2},2})$∵PC∥x轴,DC=2OB,
∴$\frac{OF}{CF}$=$\frac{OB}{CD}$=$\frac{1}{2}$,
∴CF=2OF,
由直线y=x-2可知F(0,-2),
∴OF=2,
∴CF=4,
∴C的坐标为(0,2)或(0,-6),
∴P的纵坐标为2或-6,
代入y=$\frac{3}{x}$得,2=$\frac{3}{x}$,解得x=$\frac{3}{2}$,
-6=$\frac{3}{x}$,解得x=-$\frac{1}{2}$,
∴P($\frac{3}{2}$,2)或(-$\frac{1}{2}$,-6).
故答案为P($\frac{3}{2}$,2)或(-$\frac{1}{2}$,-6).
点评 本题考查了用待定系数法求一次函数的解析式和反比例函数的解析式,一次和图象上点的坐标特征,平行线分线段成比例定理的应用,求得直线CD与y轴的交点坐标是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
6.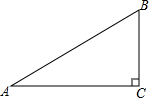 如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )
 如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )| A. | ∠B=60° | B. | a=5 | C. | b=5$\sqrt{3}$ | D. | tanB=$\frac{\sqrt{3}}{3}$ |
13.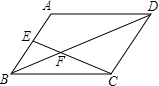 如图,在?ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCF的面积比为( )
如图,在?ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCF的面积比为( )
 如图,在?ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCF的面积比为( )
如图,在?ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCF的面积比为( )| A. | $\frac{4}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
1.已知:△ABC是一个任意三角形,用直尺和圆规作出∠A,∠B的平分线,如果两条平分线交于点O,下列选项中不正确的是( )
| A. | 点O到△ABC的三顶点的距离一定相等 | |
| B. | ∠C的平分线一定经过点O | |
| C. | 点O到△ABC的三边距离一定相等 | |
| D. | 点O一定在△ABC的内部 |
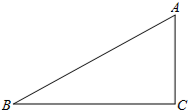 如图,在Rt△ABC中,∠C=90°,AC=3,tanB=$\frac{1}{2}$.
如图,在Rt△ABC中,∠C=90°,AC=3,tanB=$\frac{1}{2}$.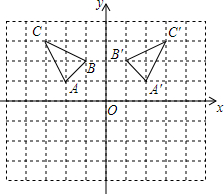 如图是一个8×10正方形格纸,△ABC中A点坐标为(-2,1).
如图是一个8×10正方形格纸,△ABC中A点坐标为(-2,1).