题目内容
19.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.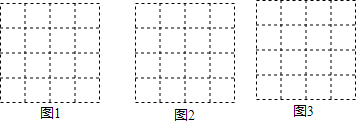
(1)在图1中,画一个三角形,使它的三边长都是有理数;
(2)在图2、图3中,分别画一个直角三角形,使它们的三边长都是无理数,并且要求所画的两个直角三角形不全等.
分析 (1)画一个边长为3,4,5的三角形即可;
(2)画一个边长为$\sqrt{2}$,2$\sqrt{2}$,$\sqrt{10}$和边长为$\sqrt{5}$,$\sqrt{5}$,$\sqrt{10}$的直角三角形即可.
解答 解(1)∵$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴画一个边长为3,4,5的三角形,
如图1所示;
(2)∵($\sqrt{2}$)2+(2$\sqrt{2}$)2=($\sqrt{10}$)2,
($\sqrt{5}$)2+($\sqrt{5}$)2=($\sqrt{10}$)2,
∴直角三角形如图2、图3所示.
点评 此题主要考查了利用勾股定理画图,关键是计算出所画图形的边长是直角边长为多少的直角三角形的斜边长.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
10.已知一次函数y=-2x-2.
(1)根据关系式画出函数的图象.
(2)求出图象与x轴、y轴的交点A、B的坐标.
(3)求A、B两点间的距离.
(4)求出△AOB的面积.
(5)y的值随x值的增大怎样变化?
(1)根据关系式画出函数的图象.
(2)求出图象与x轴、y轴的交点A、B的坐标.
(3)求A、B两点间的距离.
(4)求出△AOB的面积.
(5)y的值随x值的增大怎样变化?
7.已知(a+3)2+|b-2|=0,则2ab的值是( )
| A. | -6 | B. | 18 | C. | -12 | D. | 9 |
11.已知P1(-3,y1),P2(-3,y2)是一次函数y=2x-b的图象上的两个点,则y1、y2的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能确定 |
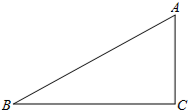 如图,在Rt△ABC中,∠C=90°,AC=3,tanB=$\frac{1}{2}$.
如图,在Rt△ABC中,∠C=90°,AC=3,tanB=$\frac{1}{2}$.