Question

9．已知抛物线的顶点坐标为（-1，-2），且抛物线过点（-2，-1）．
（1）确定抛物线的解析式；
（2）画出这个函数的图象．

Answer 1

分析 （1）设顶点式y=a（x+1）²-2，然后把（-2，-1）代入求出a即可；
（2）利用描点法法画出二次函数图象．

解答 解：（1）设抛物线解析式为y=a（x+1）²-2，
把（-2，-1）代入得a（-2+1）²-2=-1，解得a=1，
所以抛物线解析式为y=（x+1）²-2；
（2）如图，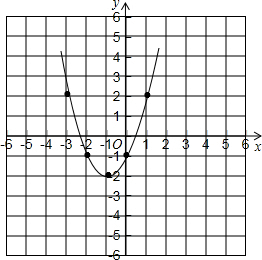

点评 本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．