题目内容
14.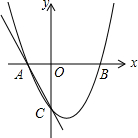 如图,二次函数y=x2+bx+c的图象交x轴于A、B两点(A、B分别在原点左、右两侧),交y轴负半轴于点C,且OB=OC=2OA.求二次函数的解析式.
如图,二次函数y=x2+bx+c的图象交x轴于A、B两点(A、B分别在原点左、右两侧),交y轴负半轴于点C,且OB=OC=2OA.求二次函数的解析式.
分析 先用c表示C点坐标,再利用OB=OC=2OA得到B(-c,0),A($\frac{1}{2}$c,0),则可设交y=(x+c)(x-$\frac{1}{2}$c),然后展开后得到关于c的方程,再解方程求出c即可得到抛物线解析式.
解答 解:当x=0时,y=x2+bx+c=c,则C(0,c),c<0,
∵OB=OC=2OA,
∴B(-c,0),A($\frac{1}{2}$c,0),
设抛物线为y=(x+c)(x-$\frac{1}{2}$c),
即y=x2+$\frac{1}{2}$cx-$\frac{1}{2}$c2,
∴-$\frac{1}{2}$c2=c,解得c1=0(舍去),c2=-2,
∴二次函数解析式为y=x2-x-2.
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.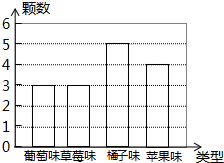 小林给弟弟买了一些糖果,放到一个不透明的袋子里,这些糖果除了口味和外包装的颜色外其余都相同,袋子里各种口味糖果的数量统计如图所示,他让弟弟从袋子里随机摸出一颗糖果.则弟弟恰好摸到橘子味糖果的概率是( )
小林给弟弟买了一些糖果,放到一个不透明的袋子里,这些糖果除了口味和外包装的颜色外其余都相同,袋子里各种口味糖果的数量统计如图所示,他让弟弟从袋子里随机摸出一颗糖果.则弟弟恰好摸到橘子味糖果的概率是( )
 小林给弟弟买了一些糖果,放到一个不透明的袋子里,这些糖果除了口味和外包装的颜色外其余都相同,袋子里各种口味糖果的数量统计如图所示,他让弟弟从袋子里随机摸出一颗糖果.则弟弟恰好摸到橘子味糖果的概率是( )
小林给弟弟买了一些糖果,放到一个不透明的袋子里,这些糖果除了口味和外包装的颜色外其余都相同,袋子里各种口味糖果的数量统计如图所示,他让弟弟从袋子里随机摸出一颗糖果.则弟弟恰好摸到橘子味糖果的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{15}$ |
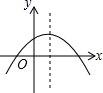 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$的大致图象是( )
二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$的大致图象是( )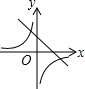

 如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.
如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.