题目内容
19. 如图,E、F分别是?ABCD的边BC、AD上的两点,∠AEB=∠FCB.求证:BE=DF.
如图,E、F分别是?ABCD的边BC、AD上的两点,∠AEB=∠FCB.求证:BE=DF.
分析 根据平行四边形的性质得出AB=CD,∠B=∠D,根据AAS证出△ABE≌△CDF即可推出答案.
解答 证明:
∵四边形ABCD为平行四边形,
∴AB=CD,∠B=∠D.
又AD∥CB,
∴∠DFC=∠FCB,
又∵∠AEB=∠FCB,
∴∠AEB=∠CFD.
在△ABE和△CDF中,
$\left\{\begin{array}{l}{∠B=∠D}\\{∠BEA=∠CFD}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△CDF(AAS),
∴BE=DF.
点评 本题主要考查对平行四边形的性质,全等三角形的性质和判定等知识点的理解和掌握,能根据性质证出△ABE≌△CDF是证此题的关键.

练习册系列答案
相关题目
10.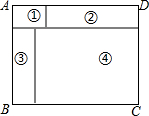 如图,矩形ABCD,由四块小矩形拼成(四块小矩形放置是既不重叠,也没有空隙),其中②③两块矩形全等,如果要求出①④两块矩形的周长之和,则只要知道( )
如图,矩形ABCD,由四块小矩形拼成(四块小矩形放置是既不重叠,也没有空隙),其中②③两块矩形全等,如果要求出①④两块矩形的周长之和,则只要知道( )
 如图,矩形ABCD,由四块小矩形拼成(四块小矩形放置是既不重叠,也没有空隙),其中②③两块矩形全等,如果要求出①④两块矩形的周长之和,则只要知道( )
如图,矩形ABCD,由四块小矩形拼成(四块小矩形放置是既不重叠,也没有空隙),其中②③两块矩形全等,如果要求出①④两块矩形的周长之和,则只要知道( )| A. | 矩形ABCD的周长 | B. | 矩形②的周长 | C. | AB的长 | D. | BC的长 |
7.鹿山广场,位于嵊州老城区真正核心地段,东临嵊州大道,南接江滨东路,西邻官河路,北镶城中路,总建筑面积达260000平方米,由情景步行街、国际名品天街、国商购物城、影视娱乐城、美食文化广场、健身休闲中心组成的一站式购物中心,及高尚湖景大宅,鼎成城市中心地标级综合体.用科学记数法将数260000表示为( )
| A. | 2.6×106 | B. | 26×104 | C. | 2.6×105 | D. | 26×105 |
14.下列代数式中,属于分式的是( )
| A. | -3 | B. | $\frac{1}{2}a-b$ | C. | $\frac{1}{x}$ | D. | -4a3b |
 如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.
如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.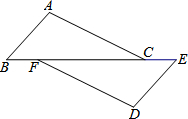 已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF.
已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF.