Question

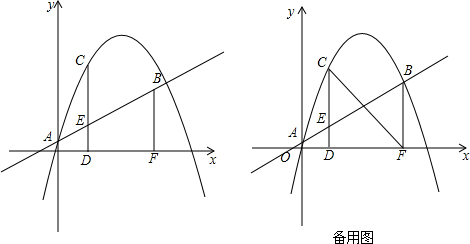
4．如图，二次函数y=ax²+bx+c与直线y=$\frac{1}{2}x+1$相交于A、B两点，A点在y轴上，当x=6时，二次函数有最大值，最大值为10，点C是二次函数图象上一点（点C在AB上方），过C作CD⊥x轴，垂足为点D，交AB于点E，过点B作BF⊥x轴，垂足为点F．
（1）求二次函数的表达式；
（2）当点C在何位置时，线段CE有最大值？请求出点C的坐标及CE的最大值；
（3）当点C在何位置时，线段BE与线段CF互相平分？请求出点C的坐标．

Answer 1

分析 （1）根据自变量与函数值的对应关系，可得A点坐标，根据待定系数法，可得函数解析式；
（2）根据平行于y轴两点之间的距离是减较小的纵坐标，可得二次函数，根据二次函数的性质，可得答案；
（3）根据解方程组，可得B点坐标，根据平行四边形的判定与性质，可得关于关于x的方程，根据自变量与函数值的对应关系，可得C点坐标．

解答 解：（1）将x=0代入y=$\frac{1}{2}$x+1，得y=1．
∴点A（0，1）．
设二次函数的表达式为y=a（x-6）²+10，
将x=0，y=1代入，得a=-$\frac{1}{4}$
∴y=-$\frac{1}{4}$（x-6）²+10．
即y=-$\frac{1}{4}$x²+3x+1．
（2）点C在抛物线上，点E在AB上，设C点坐标为（m，-$\frac{1}{4}$m²+3m+1），E（m，$\frac{1}{2}$m+1）
y_CE=-$\frac{1}{4}$m²+3m+1-$\frac{1}{2}$m-1=-$\frac{1}{4}$m²+$\frac{5}{2}$m
x=5时，y_CE最大=$\frac{25}{4}$．
将m=5代入y=-$\frac{1}{4}$x²+3m+1，得y=$\frac{39}{4}$．
∴当点C的坐标为（5，$\frac{39}{4}$）时，y_CE最大=$\frac{25}{4}$．
（3）$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{y=-\frac{1}{4}{x}^{2}+3x+1}\end{array}\right.$
解，得x₁=0，x₂=10．
将x=10代入y=$\frac{1}{2}$x+1=6，
∴BF=6．
∵线段BE与线段CF互相平分，
∴四边形BCEF是平行四边形．
∴CE=BF=6．
即-$\frac{1}{4}$x²+$\frac{5}{2}$x=6．
解，得x₁=4，x₂=6．
将x₁=4，x₂=6，分别代入y=-$\frac{1}{4}$x²+3x+1．
得y₁=9，y₂=10．
∴当点C的坐标为（4，9）或（6，10）时，线段BE与线段CF互相平分．

点评 本题考查了二次函数综合题，利用待定系数法求函数解析式；利用平行于y轴两点之间的距离是减较小的纵坐标得出二次函数是解题关键；利用平行四边形的判定与性质得出关于关于x的方程是解题关键．