题目内容
 如图所示,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于点E,若AB=10cm.
如图所示,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于点E,若AB=10cm.(1)求AC的长;
(2)求△BDE的周长.
考点:角平分线的性质,等腰直角三角形
专题:
分析:(1)设AC=xcm,则BC=AC=xcm.在直角△ABC中,利用勾股定理得出AC2+BC2=AB2,即x2+x2=102,解方程即可求解;
(2)根据角平分线上的点到角的两边的距离相等可得CD=ED,再利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应边相等可得AC=AE,然后求出△DEB的周长=AB=10cm.
(2)根据角平分线上的点到角的两边的距离相等可得CD=ED,再利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应边相等可得AC=AE,然后求出△DEB的周长=AB=10cm.
解答:解:(1)设AC=xcm,则BC=AC=xcm.
∵在△ABC,∠C=90°,
∴AC2+BC2=AB2,即x2+x2=102,
解得x=5
,
故AC的长为5
cm;
(2)∵AD是∠BAC的平分线,DE⊥AB于E,∠C=90°,
∴CD=ED.
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
又∵AC=BC,
∴△BDE的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB=10cm.
∵在△ABC,∠C=90°,
∴AC2+BC2=AB2,即x2+x2=102,
解得x=5
| 2 |
故AC的长为5
| 2 |
(2)∵AD是∠BAC的平分线,DE⊥AB于E,∠C=90°,
∴CD=ED.
在Rt△ACD和Rt△AED中,
|
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
又∵AC=BC,
∴△BDE的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB=10cm.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,全等三角形的判定与性质,勾股定理,难度适中,求出△DEB的周长=AB是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某商场四月份的利润是28万元,预计六月份的利润将达到40万元.设利润每月平均增长率为x,则根据题意所列方程正确的是( )
| A、28(1+x)2=40 |
| B、28(1+x)2=40-28 |
| C、28(1+2x)=40 |
| D、28(1+x2)=40 |
一件工作由一个人做需要20天完成,现由3人做2天,若剩下的工作要在2天内完成,则应增加(每个人的工作效率相同)的人数是( )
| A、2人 | B、3人 | C、4人 | D、5人 |
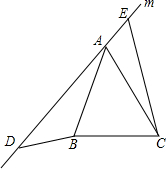 如图,在等腰三角形ABC中,已知AB=AC,∠BAC=α°,在过点A的直线m上取两点D,E,使得∠ADB=α°,∠AEC=α°.
如图,在等腰三角形ABC中,已知AB=AC,∠BAC=α°,在过点A的直线m上取两点D,E,使得∠ADB=α°,∠AEC=α°. 如图,在矩形ABCD中,两只蚂蚁P、Q同时从B点出发,分别沿BA、BC方向爬行,速度为50cm/min,若哪只蚂蚁爬到各自所在的线段的另一点时,就都停止爬行,几分钟后△PBQ的面积占矩形ABCD面积的
如图,在矩形ABCD中,两只蚂蚁P、Q同时从B点出发,分别沿BA、BC方向爬行,速度为50cm/min,若哪只蚂蚁爬到各自所在的线段的另一点时,就都停止爬行,几分钟后△PBQ的面积占矩形ABCD面积的